
Deze samenvatting is gebaseerd op het studiejaar 2013-2014.
Deel I: Inleiding
Wet van één prijs
Dit boek richt zich op hoe je optimale financiële beslissingen van de corporatie kunt nemen. Eerst wordt de corporatie geïntroduceerd en vervolgens wordt er ingegaan op gerelateerde bedrijfsvormen.
Hoofdstuk 1: De corporatie
Het eigendom van de corporatie is privé en wordt beschermd door de grondwet. Eén van de succesfactoren van de corporatie is de bekwaamheid om gemakkelijk te kunnen handelen in eigendomsaandelen.
1.1 Vier typen van ondernemingen
Er zijn vier belangrijke typen ondernemingen namelijk:
eenmanszaak
vennootschap (onder firma)
vennootschap met beperkte aansprakelijkheid (bijvoorbeeld de BV)
corporatie
Ad a. Eenmanszaken:
Een eenmanszaak is een zaak dat eigendom is en geleid wordt door één persoon. Een dergelijke zaak is vaak erg klein en heeft geen of slechts enkele werknemers. Hoewel deze bedrijfsvorm niet veel bijdraagt aan de verkoopopbrengsten binnen de economie, is het toch de meest voorkomende bedrijfsvorm in de wereld. Het voordeel van een eenmanszaak is dat het eenvoudig op te zetten is. De basisbeperking van een eenmanszaak is, dat er geen scheiding is tussen de onderneming en de eigenaar en daarom heeft een dergelijke onderneming slechts één eigenaar.
Ad b. Vennootschap (onder firma):
Een vennootschap is net een eenmanszaak, maar met meer dan één eigenaar. Bij een partnerschap zijn alle partners aansprakelijk voor de schulden van de onderneming.
Een commanditaire vennootschap is een partnerschap met twee soorten eigenaren namelijk, algemeen eigenaar en beperkt eigenaar (een medegerechtigde).
Algemene eigenaren zijn persoonlijk aansprakelijk voor de schulden en verplichtingen van de onderneming. medegerechtigden daarentegen hebben beperkte aansprakelijkheid, dat wil zeggen dat hun aansprakelijkheid beperkt is tot hun investering. Het belang of het aandeel van een beperkte eigenaar is overdraagbaar. Een beperkte eigenaar heeft geen managementbevoegdheid.
Ad c. Vennootschap met beperkte aansprakelijkheid (bijvoorbeeld de BV):
Een vennootschap met beperkte aansprakelijkheid is een beperkte partnerschap zonder een algemene eigenaar (partner). Dat houdt in dat alle eigenaren beperkte aansprakelijkheid hebben, maar anders dan bij beperkte eigenaren kunnen zij wél de zaak leiden (het management).
Ad d. Corporatie:
Een onderscheidend kenmerk van een corporatie is dat het een wettelijk bepaald kunstmatig bestaan heeft, gescheiden van zijn eigenaren. Een corporatie kan contracten aangaan, bezittingen verkrijgen en zich aansprakelijk stellen voor verplichtingen.
Daarnaast krijgt een corporatie bescherming vanuit de Amerikaanse grondwet tegen inbeslagneming van haar eigendom.
Aangezien een corporatie een wettelijke entiteit is, gescheiden en verschillend van haar eigenaren, is zij alleen verantwoordelijk voor haar eigen verplichtingen. Dit houdt in dat de eigenaren van een corporatie niet aansprakelijk zijn voor de verplichtingen die de corporatie aangaat. De corporatie is ook niet aansprakelijk voor de persoonlijke verplichtingen van haar eigenaren.
Eigendom van een corporatie
Er is geen limiet aan het aantal eigenaren dat een corporatie kan hebben. De gehele participatie van het eigendom van een corporatie wordt verdeeld in delen, genaamd aandelen. De verzameling van alle uitstaande aandelen van een corporatie wordt het Eigen Vermogen (EV) van de corporatie genoemd.
Een eigenaar van een aandeel wordt een aandeelhouder of een vermogenshouder genoemd, en heeft recht op een dividenduitkering. Dividenduitkeringen zijnalle uitkeringen die voortvloeien uit de uitvoering van het beleid van de corporatie ten behoeve van de aandeelhouders. De aandelen van de corporatie zijn vrij verhandelbaar waardoor geld van externe investeerders aangetrokken kan worden. Door de beschikbaarheid van externe investeerders zijn de corporaties in staat om de economie te domineren (voorbeeld Microsoft).
Belasting implicaties voor corporatie entiteiten
Een belangrijk verschil tussen de vier organisatietypen is de manier waarop zij belast worden. Omdat een corporatie een afzonderlijke wettelijke entiteit is, zijn de opbrengsten van een corporatie onderhevig aan belastingen afzonderlijk van de belastingverplichtingen van haar eigenaren. In principe betalen aandeelhouders van een corporatie twee keer belasting namelijk belasting op de opbrengst van de corporatie én hun eigen inkomstenbelasting verkregen uit de opbrengstuitkering van de corporatie. Dit noemen wij een C-corporatie en werkt volgens het ‘klassieke systeem’ van dubbele taxatie.
Een S-corporatie wil zeggen dat deze corporaties zijn vrijgesteld voor het betalen van de corporatiebelasting. De opbrengsten van de S-corporatie worden niet belast, maar direct uitgekeerd aan de aandeelhouders op basis van hun aandeel. Vervolgens moeten deze aandeelhouders zelf inkomstenbelasting betalen. Dit alternatief heet het imputatiesysteem.
1.2 Eigendom versus controle over de corporatie
In tegenstelling tot een eenmanszaak waar de eigenaar direct controle heeft over de organisatie, is het vaak voor de eigenaren van de corporatie onuitvoerbaar om direct controle uit te kunnen oefenen op de organisatie, omdat er sprake is van veel eigenaren die hun aandelen vrij kunnen verhandelen. Daarom zijn bij een corporatie ‘directe controle’ en ‘eigendom’ vaak gescheiden.
Het managementteam van een corporatie
De aandeelhouders van een corporatie oefenen indirect hun invloed uit door het kiezen van een Raad van Bestuur, dat is een groep mensen die de ultieme bevoegdheid heeft om te beslissen over de corporatie. De president directeur (CEO) is verantwoordelijk voor het leiden van de organisatie door het vaststellen van regels en het beleid. De CFO rapporteert direct aan de CEO.
De financiële managers hebben 3 hoofdtaken:
Investeringsbeslissingen nemen door het afwegen van kosten en opbrengsten
Financieringsbeslissingen nemen over hoe de investeringen gefinancierd moeten worden
De kas beheren om alle verplichtingen na te kunnen komen en het bedrijfskapitaal te managen
Eigendom en controle over corporaties
In theorie wordt het doel van een organisatie bepaald door de eigenaren. Maar een corporatie wordt bestuurd door een managementteam, los van haar eigenaren. Hoe kunnen de eigenaren van een corporatie verzekeren dat het managementteam hun doelen zal implementeren?
Door de scheiding van eigendom en controle over de corporatie, hebben managers een kleine prikkel om in het belang van de aandeelhouders te werken, wanneer dit betekent dat ze tegen hun eigen belang moeten handelen. Dit noemen we een Principaal-Agent probleem.
Aandeelhouders kunnen managers aanmoedigen om in het belang van de aandeelhouders te werken, door ze te disciplineren als ze dat niet doen. Als de aandeelhouders niet tevreden zijn met het functioneren van de algemeen directeur, dan kunnen zij hem via de Raad van Bestuur laten ontslaan.
Bij een vijandige overname kan een individu of een organisatie een groot deel van de aandelen kopen en daarmee genoeg stemmen behalen om de Raad van Bestuur en de algemeen directeur te vervangen.
Als een corporatie haar schulden niet kan terugbetalen, dan zullen de schuldeisers beslag leggen op de bezittingen van de corporatie ter compensatie van hun vorderingen. Om een inbeslagneming te vermijden, zal een corporatie via de rechter een faillissement aanvragen.
Een faillissement van een corporatie kan gezien worden als een verandering van eigendom en controle over de corporatie. De aandeelhouders geven hun eigendom en controle over aan de schuldeisers.
Een faillissement hoeft niet te resulteren in een liquidatie van de onderneming, dat wil zeggen het sluiten van het bedrijf en het verkopen van haar bezittingen.
1.3 De aandelenbeurs
Een investering wordt liquide genoemd als het mogelijk is om het weer gemakkelijk te verkopen voor een prijs, dat niet veel afwijkt van de prijs waarvoor je ze nú kan kopen. De aandelen van veel corporaties zijn liquide te noemen, omdat deze op georganiseerde markten verhandeld worden namelijk, aandelenbeurzen. Dit soort corporaties noemt men naamloze vennootschap.
Een belegger van een naamloze vennootschap kan gemakkelijk en snel zijn belegging omzetten in geld door simpelweg zijn aandelen te verkopen op een van deze markten.
Echter niet alle corporaties zijn naamloze vennootschappen. Bij sommige corporaties is het handelen in aandelen helemaal of gedeeltelijk niet toegestaan. Dit soort corporaties noemen we particuliere bedrijven.
Op de primaire markt verkoopt een bedrijf nieuwe aandelen aan investeerders, die ze vervolgens doorverhandeld op de secundaire markt.
De grootste aandelenbeurs van de wereld is de New York Stock Exchange (NYSE). De NYSE is een fysieke plaats waar specialisten kopers en verkopers bij elkaar brengen. Zij stellen twee prijzen op voor elk aandeel op de markt waarin zij opereren namelijk, de biedprijs (de prijs waartegen zij het aandeel willen kopen) en de vraagprijs (de prijs waartegen zij het aandeel willen verkopen).
De vraagprijs overschrijdt de biedprijs. Dit verschil noemen we de bied-vraag spreiding. Aangezien klanten altijd kopen tegen de vraagprijs (de hogere prijs) en verkopen tegen de biedprijs (de lagere prijs), is de bied-vraag spreiding een soort van transactiekosten die de beleggers moeten betalen om te kunnen handelen.
Hoofdstuk 2: Introductie van financiële overzichtsanalyse
Een belangrijke informatiebron is het financiële overzicht, waarin een evaluatie over het functioneren van de organisatie wordt gegeven. Een financieel overzicht dient als een communicatiemiddel voor het communiceren van financiële informatie met de beleggers.
2.1 De openbaarmaking van financiële informatie
Een financieel overzicht is een boekhoudkundig verslag met informatie over het functioneren van het bedrijf in het verleden en het wordt periodiek uitgegeven. De naamloze vennootschappen in Amerika moeten ieder jaar een jaarverslag versturen aan de aandeelhouders. Het financiële overzicht is een onderdeel van het jaarverslag.
Financiële verslagen zijn belangrijke instrumenten waarmee beleggers, financiële analisten en andere extern geïnteresseerde partijen informatie verkrijgen over een corporatie. Deze financiële overzichten zijn ook bruikbaar voor de managers van het bedrijf zelf, omdat ze een informatiebron zijn voor financiële beslissingen van de corporatie.
Voorbereiding van financiële overzichten
Een corporatie moet een accountant inhuren om de jaarlijkse financiële overzichten te checken, ofwel na te gaan of ze volgens de algemeen aanvaarde boekhoudkundige beginselen (GAAP) opgesteld zijn en verifiëren of de informatie betrouwbaar is.
Een GAAP is een raamwerk van regels en een standaard formaat voor naamloze vennootschappen voor het voorbereiden en opstellen van hun jaarlijkse verslagen.
Vier typen van financiële overzichten
Iedere naamloze vennootschap dient vier financiële verslagen op te stellen namelijk:
balans
winst- en verliesrekening
kasstroomoverzicht
mutatieoverzicht van het eigen vermogen.
2.2 De balans
De balans geeft de huidige financiële positie van een bedrijf weer voor een bepaald moment, dat wil zeggen de bezittingen en schulden van een bedrijf. Een balans is verdeeld in twee zijden: op de linkerzijde staan de bezittingen (activa) en op de rechterzijde staan de schulden (passiva). Rechts op de balans kan men het Eigen Vermogen van de aandeelhouders vinden, dat is het verschil tussen de bezittingen en de schulden van het bedrijf.
De twee zijden van de balans moeten in evenwicht zijn, dat houdt in:
Activa = Passiva + EV, dus EV = bezittingen – schulden
Activa
Activa zijn onder te verdelen in:
Vlottende activa: geld of vordering die binnen één jaar in contant geld omgezet kan worden.
Lange termijn activa: dit zijn activa die langer dan één jaar meegaan (bijvoorbeeld machines).
De vlottende activa kunnen verder onderverdeeld worden in beschikbare waarden (korte termijn investeringen met weinig risico), de te ontvangen rekeningen, voorraden, en overige activa zoals vooruitbetaalde kosten.
Afschrijving is niet een echte uitgave in geld die het bedrijf moet betalen, maar het is de wijze waarop aangegeven wordt dat gebouwen en andere uitrusting verslijten en daarmee minder waard zijn door veroudering.
De boekwaarde van een goed is gelijk aan de verwervingskosten minus cumulatieve afschrijvingen.
Voorbeeld: Er wordt aan het begin van jaar 1 een computer gekocht voor €2.000 door het bedrijf. De computer wordt in 5 jaar afgeschreven tot nihil. De jaarlijkse afschrijving is dus (2000/5) = €400. Eind jaar 1 bedraagt de boekwaarde €1.600 (= 2000 – 400). Eind jaar 5 bedraagt de boekwaarde van de computer €0, terwijl de activa wel voor een hogere prijs kan worden verkocht.
Passiva
Ook de passiva kunnen onderverdeeld worden in:
Kortlopende schulden: dat zijn schulden die binnen een jaar voldaan zullen worden.
Langlopende schulden: schulden die langer dan een jaar zullen uitstaan.
Het verschil tussen kortlopende en langlopende schulden is het netto werkkapitaal van een bedrijf, dat is kapitaal dat op korte termijn beschikbaar is om het bedrijf draaiende te houden.
Eigen Vermogen van de aandeelhouders
Het verschil tussen de activa en de passiva van het bedrijf noemen we het Eigen Vermogen van de aandeelhouders, ofwel de boekwaarde van het Eigen Vermogen.
De boekwaarde van het Eigen Vermogen is een onnauwkeurige schatting van de actuele waarde van het Eigen Vermogen van het bedrijf, omdat:
de activa die op de balans staan gewaardeerd zijn op basis van hun historische kostprijs, in plaats van hun huidige werkelijke waarde.
veel waardevolle activa van het bedrijf staan niet vermeld op de balans zoals, expertise van de werknemers, marktreputatie van het bedrijf enzovoort.
De totale marktwaarde van het Eigen Vermogen van een bedrijf is gelijk aan de marktprijs per aandeel vermenigvuldigd met het aantal aandelen, ook wel de beurswaarde genoemd.
De marktwaarde van een aandeel hangt niet af van de historische kosten van de activa van het bedrijf, maar hangt af van wat de beleggers verwachten dat met behulp van deze activa geproduceerd kan worden in de toekomst.
De boekwaarde van het Eigen Vermogen kan negatief zijn (passiva hoger dan activa), maar dat wil niet zeggen dat het bedrijf slecht functioneert.
2.3 Analyse van de balans
De liquiditeitswaarde van een bedrijf is de waarde die overblijft als haar activa verkocht zouden worden en haar schulden betaald zouden worden.
Marktboekwaarde ratio = Marktwaarde van het EV / Boekwaarde van het EV
De marktboekwaarde ratio bij een succesvol bedrijf is hoger dan één. Bedrijven met een lage marktboekwaarde ratio worden ook wel ‘waarde aandelen’ genoemd en bedrijven met een hoge marktboekwaarde ratio worden ‘groeiaandelen’ genoemd.
Vanuit de balans kunnen we ook het hefboomeffect van een bedrijf bepalen. Het hefboomeffect is de mate waarin een bedrijf zich beroept op schulden als een bron voor financiering. De schulden/EV ratio is een ratio dat gebruikt wordt voor het schatten van het hefboomeffect van een bedrijf.
Schulden/EV ratio = Totale schulden / Totaal Eigen Vermogen
De bedrijfswaarde van een bedrijf is de totale waarde van haar onderliggende bedrijfsoperaties. We kunnen ook zeggen dat de bedrijfswaarde aangeeft wat de kosten zijn om een bedrijf over te nemen. De bedrijfswaarde bereken je door de volgende formule:
Bedrijfswaarde = Marktwaarde EV + Schulden – Kasgeld
Crediteuren vergelijken vaak de activa en passiva van bedrijven, samengevat in een bedrijfskapitaalratio of quick ratio. Hoe hoger de ratio, hoe minder risico het bedrijf loopt om tekorten te ervaren.
2.4 Winst- en verliesrekening
De winst- en verliesrekening geeft de opbrengsten en uitgaven van een bedrijf weer over een tijdsperiode en het berekent de ondergrens van het netto inkomen of de inkomsten.
Winst berekening
Brutowinst is het verschil tussen opbrengsten en kosten.
Netto inkomen geeft de totale opbrengsten weer van de aandeelhouders van het bedrijf. Het wordt vaak per aandeel aangegeven als de winst per aandeel (EPS).
Winst per aandeel = netto inkomen / uitstaande aandelen
Een aandelenoptie geeft de houder ervan het recht om een zeker aantal aandelen te kopen voor een specifieke prijs. Via aandelenopties kan het aantal uitgebrachte aandelen groeien. Het aantal aandelen kan ook groeien als het bedrijf converteerbare obligaties uitgeeft, dat is een vorm van schuld dat omgezet kan worden in aandelen.
Verwaterde winst per aandeel geeft de winst per aandeel aan, die het bedrijf zou krijgen als de aandelenopties uitgeoefend worden.
2.5 Winst- en verliesrekeninganalyse
De winst- en verliesrekening verschaft erg bruikbare informatie ten aanzien van de winstgevendheid van een bedrijf en hoe het zich verhoudt met de waarde van de aandelen van een bedrijf.
Er zijn een aantal ratio’s te noemen waarmee het functioneren en de waarde van een bedrijf berekend kan worden.
Als eerste kijken we naar twee winstgevendheid ratio’s namelijk,
Operationele marge = bedrijfsopbrengsten / totale verkoop . De operationele marge is de ratio van bedrijfsopbrengsten ten opzichte van de verkoopopbrengsten.
Nettowinst marge = Netto-inkomen / Totale verkoop. De nettowinst marge is de ratio van het netto-inkomen ten opzichte van de totale verkoop. Deze geeft elke fractie van een euro in opbrengsten aan, dat beschikbaar is voor de aandeelhouders ná rente en belastingen.
Winstgevendheid ratio’s zijn een indicatie voor de efficiency van een bedrijf en haar prijsstrategie.
‘Werkkapitaal dagen’ is het uitdrukken van debiteuren in termen van het aantal dagen van de verkoopwaarde dat het representeert.
Debiteuren dagen = Debiteuren / Gemiddelde dagelijkse omzet.
Werkkapitaal ratio’s drukken het werkkapitaal van een bedrijf uit als het aantal dagen van de verkoop (vorderingen) of kosten van de verkoop (schulden).
Financiële analisten berekenen vaak de inkomsten van een bedrijf vóór rente, belasting, afschrijving en aflossing.
Een rentedekking ratio is een voorbeeld van een hefboomeffect ratio. Geldverstrekkers meten het hefboomeffect van een bedrijf vaak af door het berekenen van een rentedekking ratio.
Een rentedekking ratio geeft de ratio van de bedrijfsinkomsten (of cash flows) ten opzichte van haar rente-uitgaven. Deze ratio’s zijn een maatstaf voor de financiële sterkte van een bedrijf. Wanneer deze ratio hoog is, betekent dit dat het bedrijf veel meer verdient dan noodzakelijk is om aan haar vereiste rentebetalingen te kunnen voldoen.
Analisten evalueren vaak de beleggingsopbrengsten van een bedrijf door haar inkomen te vergelijken met haar investeringen.
Daarvoor gebruiken zij het zogenaamde rendement op het Eigen Vermogen (ROE).
Rendement op EV = Netto inkomen / Boekwaarde van het EV
Deze ratio verschaft een maatstaf voor het rendement dat het bedrijf heeft verdiend op haar investeringen in het verleden.
Een hoog rendement op het EV houdt in dat het bedrijf in staat is om investeringskansen te vinden die erg winstgevend zijn.
Een andere maatstaf is rendement op activa (ROA) dat wil zeggen:
Rendement op activa = Netto inkomen / Totale activa
Analisten gebruiken ook een aantal ratio’s voor het peilen van de marktwaarde van een bedrijf. Deze ratio’s noemen we waarderingsratio’s. De belangrijkste is de prijswinstverhouding (P/E ratio) van het bedrijf.
Prijswinstverhouding = Beurswaarde / Netto inkomen.
We kunnen de prijswinstverhouding ook per aandeel berekenen, namelijk
Prijswinstverhouding per aandeel = Aandelenkoers / Winst per aandeel.
De prijswinstverhouding is niet bruikbaar als de inkomsten van het bedrijf negatief zijn. In dit geval is het gebruikelijk om te kijken naar de bedrijfswaarde van het bedrijf gerelateerd aan de verkoop.
2.6 Cash flow overzicht
Een overzicht van de cash flows benut de informatie uit een winst- en verliesrekening en de balans om vast te stellen hoeveel geld het bedrijf gegenereerd heeft en hoe dat geld toegewezen is gedurende een bepaalde periode.
Een cash flow overzicht is onder te verdelen in drie delen:
Bedrijfsactiviteit: dit begint met het netto-inkomen uit een winst- en verliesrekening. Dit aantal wordt weer aangepast door het toevoegen van alle non-cash onderdelen gerelateerd aan de bedrijfsactiviteit van de onderneming.
Investeringsactiviteit: dit geeft het geld aan dat voor investeringen wordt gebruikt. De aankoop van nieuwe machines, pand en dergelijke valt hieronder.
Financieringsactiviteit: dit geeft de geldstroom aan tussen het bedrijf en haar investeerders.
Het verschil tussen het netto-inkomen en het bedrag dat een bedrijf uitgeeft aan dividend, wordt de ingehouden winst voor dat jaar genoemd.
Ingehouden winst = Netto-inkomen – Dividend
2.7 Andere financiële informatieoverzichten
In het financiële overzicht staan ook andere elementen vermeld zoals managementdiscussie en -analyse, staat van het Eigen Vermogen van de aandeelhouders en opmerkingen ten aanzien van het financiële overzicht.
Managementdiscussie en -analyse
De managementdiscussie en -analyse van het financiële overzicht bevat een managementoverzicht over het functioneren van het bedrijf, als wel een openbaarmaking van de risico’s waar het bedrijf mee te maken heeft, inclusief de risico’s van transacties die buiten de balans vallen.
Staat van het Eigen Vermogen van de aandeelhouders
De staat van het Eigen Vermogen van de aandeelhouders ontleedt het Eigen Vermogen van de aandeelhouders, dat op de balans aangegeven is in het bedrag dat tot stand kwam door het uitgeven van nieuwe aandelen versus ingehouden winst.
Opmerkingen ten aanzien van het financiële overzicht
Bedrijven vermelden vaak uitgebreide opmerkingen met nadere details op de informatie die in de overzichten staat.
2.8 Boekhoudkundige manipulatie
Recente boekhoudkundige schandalen hebben in Amerika de aandacht gevestigd op het belang van financiële overzichten. De nieuwe wetgeving vereist dat de algemeen directeur en financieel directeur de nauwkeurigheid en geschiktheid van financiële overzichten van hun bedrijf laten certificeren. Door deze nieuwe wetgeving zijn de straffen voor fraude toegenomen en zijn de procedures, die de bedrijven moeten volgen om te verzekeren dat overzichten nauwkeurig zijn, verscherpt. Dit is het Sarbanes-Oxley Act (SOX).
Hoofdstuk 3: Arbitrage en financiële besluitvorming
Elke beslissing heeft consequenties voor de toekomst en deze consequenties kunnen voordelig of nadelig zijn. Als de extra kosten de voordelen overschrijden, dan zal de beslissing om te investeren de waarde van het bedrijf verhogen en daarmee ook de welvaart van haar investeerders.
Het verschil tussen de contante waarde van de baten en de kosten geeft het nettobedrag aan, waarmee de beslissing de welvaart zal doen toenemen.
3.1 Waardering van kosten en baten
De eerste stap in het evalueren van een project is het identificeren van haar kosten en baten.
De financiële manager moet eerst de kosten en baten van het project kwantificeren en vervolgens overwegen of de investeringskans waardevol is of niet.
Marktprijzen gebruiken voor vaststellen van contante waarde
Om kosten en baten, die op verschillende tijdstippen voorkomen, in verschillende valuta uitgedrukt worden of een verschillend risico hebben, te kunnen vergelijken moeten we alle kosten en baten in algemene termen noteren. We rekenen de kosten en baten om in contanten ‘vandaag’.
Een concurrentiemarkt is een markt waarop een goed gekocht en verkocht kan worden tegen dezelfde prijs. We gebruiken de prijzen van een concurrentiemarkt om de contante waarde van een goed te bepalen.
3.2 Rentevoet en tijdswaarde van geld
Voor de meeste financiële beslissingen geldt dat de kosten en baten zich op verschillende tijdstippen voordoen. Hierdoor moet je rekening houden met het tijdsverschil om een project te evalueren.
De tijdswaarde van geld
Het verschil in waarde tussen geld vandaag en geld in de toekomst is de tijdswaarde van geld. Je kunt bijvoorbeeld € 1,00 investeren tegen 7% rente, dan heb je aan het eind van het jaar € 1,07 verdiend. Dit noemen we de tijdswaarde van geld.
De rentevoet: een wisselkoers in de tijd
De koers waartegen wij geld vandaag kunnen inwisselen voor geld in de toekomst door te lenen of te investeren, noemen we de huidige markt rentevoet. De rentevoet maakt het mogelijk om geld vanaf een bepaald tijdstip om te rekenen naar een ander tijdstip. Het vertelt ons de marktprijs van vandaag, van geld in de toekomst.
De risicovrije rentevoet rƒ, is de koers waartegen geld geleend en uitgeleend kan worden zonder enkel risico. We kunnen (1 + rƒ) euro’s inwisselen in euro’s in de toekomst per euro vandaag, en vice versa, zonder enig risico. De factor (1 + rƒ) noemen we de rente factor.
De factor 1 / (1 + r) noemen we de één jaar verdisconteringspercentage.
Stel: r = 7%
1 / (1 + r) = 1 / 1,07 = 0,93458 dat is de prijs die je vandaag voor € 1,00 over één jaar krijgt.
Deze waarde is lager dan € 1,00 dat wil zeggen dat geld in de toekomst, vandaag minder waard is dus de prijs ervan geeft een ‘korting’ weer.
De risicovrije rentevoet wordt ook wel de verdisconteringsvoet voor een risicovrije investering genoemd.
3.3 Contante waarde en de Netto contante waarde
De waarde van de kosten of baten wordt berekend in termen van geld vandaag, dit noemen we de contante waarde (CW)
Netto contante waarde
De netto contante waarde (NCW) van een project of investering is het verschil tussen de contante waarde van de kosten van deze investering:
Netto contante waarde = Contante waarde (Baten) – Contante waarde (Kosten).
Stel: in ruil voor € 500 vandaag krijg je € 550 over één jaar met zekerheid. Als de risicovrije rentevoet 8% per jaar is, dan geldt:
CW (Baten) = (€ 550 over een jaar) ÷ (1,08 € over een jaar / € vandaag) = € 509,26 vandaag.
Dus € 509,26 is het bedrag dat we vandaag op de bank moeten zetten om € 550 over één jaar te kunnen genereren (= € 509,26 x 1,08 = € 550).
De netto contante waarde beslissingsregel
De netto contante waarde representeert de waarde van het project in termen van geld vandaag.
Goede projecten hebben een positieve netto contante waarde, dus de welvaart van de investeerder neemt toe.
Projecten met negatieve netto contante waarde hebben kosten die de baten overschrijden, dat wil zeggen dat je op dat project vandaag verlies maakt als je het accepteert.
De netto contante waarde regel:
Bij het nemen van een investeringsbeslissing moet je het alternatief met de hoogste netto contante waarde nemen. Het kiezen van dit alternatief is gelijk aan het ontvangen van zijn netto contante waarde in geld vandaag.
Netto contante waarde en individuele voorkeuren
Ongeacht onze voorkeuren voor geld vandaag versus geld in de toekomst, moeten we altijd eerst de netto contante waarde maximaliseren. Pas daarna kunnen we lenen of uitlenen om de cash flow in de tijd te verplaatsen en zo het patroon van de cash flows vinden met onze hoogste voorkeur.
3.4 Arbitrage en de wet van één prijs
Arbitrage is het proces van handel om voordeel te behalen uit equivalente goederen die verschillende prijzen op verschillende concurrentiemarkten hebben.
Een arbitragemogelijkheid is elke situatie waarin het mogelijk is om winst te maken zonder enig risico te nemen of een investering te plegen.
Een arbitragemogelijkheid heeft een positieve netto contante waarde.
Een normale markt is een concurrentiemarkt zonder arbitrage mogelijkheden.
Wet van één prijs
Als de prijzen op twee markten verschillen, dan zullen investeerders meteen profiteren door te kopen op de markt dat goedkoop is, en verkopen op de markt waar de prijs hoger is. Op deze wijze zal de prijs uiteindelijk gelijk worden. Het resultaat is dus dat de prijzen niet meer verschillen, dit noemen we de wet van één prijs.
Wet van één prijs: als equivalente investeringsgoederen of -zekerheden simultaan verhandeld worden op verschillende markten, dan zullen ze op beide markten tegen dezelfde prijs verhandeld worden.
3.5 Geen arbitrage en zekerheidsprijzen
Een investeringsgelegenheid dat verhandeld wordt op een financiële markt, wordt een financiële zekerheid genoemd.
Waardering van een zekerheid
Een obligatie is een zekerheid die door de overheid wordt uitgegeven om nú geld te innen van haar investeerders in ruil voor de beloofde betaling in de toekomst.
Stel: we hebben twee mogelijkheden om dezelfde cash flow te behalen namelijk,
een obligatie kopen die over één jaar € 1000 oplevert.
geld investeren bij de bank om over één jaar € 1000 te ontvangen tegen een risicovrije rentevoet van 5%.
De contante waarde van €1000 investeren bij de bank bereken je als volgt:
De CW (€ 1000 over één jaar) = (€ 1000 over één jaar) ÷ (1,05 € over één jaar / € vandaag) = € 952,38 vandaag
Dus als we € 952,38 vandaag investeren tegen 5% risicovrije rentevoet, zullen we € 1000 over één jaar zonder enig risico ontvangen.
Omdat beide mogelijkheden dezelfde cash flow opleveren, moet volgens de wet van één prijs beiden dezelfde prijs hebben op een normale markt:
prijs (obligatie) = € 952,38
Stel: er is sprake van arbitragemogelijkheid. Als de obligatie een andere prijs had, dan zou er wel een mogelijkheid voor arbitrage zijn.
We veronderstellen dat de prijs van de obligatie € 940 is. Hoe kun je winst behalen in deze situatie?
Allereerst kun je de obligatie kopen voor € 940 en tegelijkertijd kun je € 952,38 lenen bij de bank tegen 5% risicovrije rentevoet. Over één jaar moet je de bank € 952,38 x 1,05 = € 1000 terugbetalen.
Met deze twee transacties verdien je € 12,38 nú voor elke obligatie die je koopt, zonder enig risico dat je in de toekomst zelf geld moet bijleggen. Dit is samengevat in onderstaande tabel.
Netto cash flow door het kopen van obligatie en lenen | ||
|
Vandaag (€) |
Over één jaar (€)
|
Obligatie kopen
| - 940,00 | + 1000 |
Lenen van de bank
| + 952,38 | - 1000 |
Netto cash flow
| + 12,38 | 0.00 |
Als de obligatieprijs hoger is dan € 952,38 treedt er eenzelfde arbitragemogelijkheid op.
Stel: obligatie kost € 960. In dit geval moeten we de obligatie verkopen en € 952,38 bij de bank investeren. Dit levert nú € 7,62 op (zie tabel hieronder).
Netto cash flow door het verkopen van obligatie en investeren | ||
|
Vandaag (€) |
Over één jaar (€)
|
Obligatie verkopen
| + 960,00 | - 1000 |
Investeren bij de bank
| - 952,38 | + 1000 |
Netto cash flow
| + 7,62 | 0.00 |
Vaststellen van non-arbitrage prijs
In het bovenstaande voorbeeld is de prijs van € 952,38 dié prijs waarbij géén arbitrage mogelijkheden meer bestaan voor onze obligatie.
Deze prijs noemen we de non-arbitrageprijs voor onze obligatie. De formule voor een non-arbitrage prijs van een zekerheid is:
Prijs (zekerheid) = CW (alle cash flows betaald door de zekerheid).
Vaststellen van de rentevoet uit obligatieprijzen
Als wij de prijs van een risicovrije obligatie weten, kunnen we met de bovenstaande formule vaststellen wat de risicovrije rentevoet moet zijn als er geen arbitrage mogelijkheden meer over zijn.
Stel: een risicovrije obligatie die over een jaar € 1000 oplevert, wordt nu verhandeld op een concurrentiemarkt tegen € 929,80.
We weten dat de prijs van de obligatie gelijk moet zijn aan de contante waarde van € 1000 cash flow die het oplevert:
€ 929,80 vandaag = (€1000 over een jaar) ÷ (1 + rƒ € over een jaar / € vandaag).
Uit deze vergelijking kunnen we de risicovrije rentevoet afleiden:
1 + rƒ = € 1000 over een jaar / € 929,80 vandaag = 1,0755 € over een jaar / € vandaag
Deze uitkomst geeft aan dat de risicovrije rentevoet 7,55% zal bedragen als er geen arbitragemogelijkheden meer zijn. Er dient opgemerkt te worden dat de risicovrije rentevoet gelijk is aan de procentuele winst dat je verdient door in de obligatie te investeren, dit noemen we het obligatierendement:
Obligatierendement = Verdiensten aan het eind van het jaar / Initiële kosten.
= (1000 – 929,80) / 929,80 = (1000 / 929,80) – 1 = 7,55%
Non-arbitrage is equivalent aan het idee, dat alle risicovrije investeringen dezelfde verdiensten zouden moeten opleveren voor de investeerder.
De netto contante waarde van handelbare zekerheden
Als zekerheden (effecten) verhandeld worden tegen non-arbitrage prijzen, wat is dan de waarde van het verhandelen van zekerheden?
De netto contante waarde van het kopen van een zekerheid is nul.
NCW (zekerheid kopen) = CW (alle cash flows betaald door zekerheid) – Prijs (zekerheid) = 0
Als we een zekerheid verkopen dan zijn de baten ‘de prijs die we krijgen’ en de kosten zijn ‘de cash flows die we opgeven’. Ook nu is de netto contante waarde gelijk aan nul.
NCW (verkopen zekerheid) = Prijs (zekerheid) – CW (alle cash flows betaald door zekerheid) = 0
Dus de netto contante waarde van het verhandelen van een zekerheid op een normale markt is nul, want er bestaan geen arbitragemogelijkheden op normale markten.
Het scheidingsbeginsel geeft aan dat we een scheiding moeten maken tussen de investeringsbeslissing van het bedrijf en haar financiële keuze.
Het scheidingsprincipe houdt in:
zekerheidstransacties creëren of verminderen geen waarde op zichzelf op een normale markt. Als gevolg daarvan kunnen we de netto contante waarde van een investeringsbeslissing scheiden van de zekerheidstransacties die het bedrijf overweegt.
Waardering van een portfolio
Tot nu toe hebben we alleen gekeken naar de non-arbitrage prijs van individuele zekerheden. De wet van één prijs heeft ook implicaties voor een pakket van zekerheden.
Stel: we hebben twee zekerheden A en B.
Daarnaast is er ook een derde zekerheid C, die dezelfde cash flows heeft als A en B samen. In dit geval is zekerheid C equivalent aan een portfolio ofwel een combinatie van zekerheid A en B. Wat kunnen we concluderen over de prijs van zekerheid C vergeleken met de prijzen van A en B?
Omdat zekerheid C equivalent is aan de portfolio van A en B moeten ze volgens de wet van één prijs, dezelfde prijs hebben. Deze relatie noemen we waarde toevoeging.
Dus de prijs van C moet gelijk zijn aan de prijs van de portfolio, dat wil zeggen de gecombineerde prijs van A en B.
Waarde toevoeging:
Prijs (C) = Prijs (A + B) = Prijs (A) + Prijs (B).
Aangezien zekerheid C cash flows heeft die gelijk zijn aan de som van A en B, moet haar waarde of prijs ‘de som van de waarde van A en B’ zijn.
In het algemeen houdt waarde toevoeging in dat de waarde van een portfolio gelijk is aan de som van de waarden van haar delen.
Waarde toevoeging heeft een belangrijk gevolg voor de waarde van het hele bedrijf. De prijs of waarde van het hele bedrijf is gelijk aan de som van de waarden van alle projecten en investeringen daarin.
Om de waarde van het bedrijf te kunnen maximaliseren, moeten managers dié beslissingen nemen die de netto contante waarde maximaliseren. De netto contante waarde van een beslissing representeert haar bijdrage aan de totale waarde van het bedrijf.
Hoofdstuk 4: De tijdswaarde van geld
4.1 De tijdslijn
Een serie cash flows die verschillende periodes duurt, noemen we een cash flow stroom. Een cash flow stroom kunnen we op een tijdslijn weergeven. Een tijdslijn is een lineaire tijdsweergave van de verwachte cash flows. Tijdslijnen zijn een kritieke eerste stap bij het organiseren van de cash flows bij een financieel probleem.
4.2 Drie regels voor verplaatsing in tijd
Financiële beslissingen vereisen vaak het vergelijken of combineren van cash flows, die op verschillende tijdstippen voorkomen.
Er zijn drie belangrijke regels voor het vergelijken en combineren van waarden namelijk:
Slechts cash flows die op hetzelfde tijdstip voorkomen, kunnen vergeleken en gecombineerd worden.
Om een cash flow vooruit in de tijd te kunnen verplaatsen, moet je het samengesteld maken.
om een cash flow terug in de tijd te kunnen berekenen, moet je het verdisconteren.
Ad 1: vergelijken en combineren van waarden
Een euro nú en een euro over één jaar zijn niet equivalent. Het is waardevoller om een euro nu te hebben, want dan kan je het op de bank zetten en hier rente over ontvangen.
Ad 2: cash flows vooruit in de tijd verplaatsen
Stel we hebben €1000 nu en we willen weten wat de waarde over één jaar is. Als de huidige rentevoet 10% is, kunnen we de cash flow vooruit in de tijd berekenen:
(€1000 nú) x (1,10 over een jaar / € nú ) = €1100 over een jaar
Het vermenigvuldigen met (1 + r) noemen we samengesteld maken van rente. Dit kunnen we aangeven met behulp van een tijdslijn:
0 1 2
————————————————————————— Tijdslijn
€1000 → €1100 → €1210
x 1,10 x 1,10
De toekomstige waarde (TW) is de waarde van een cash flow die vooruit in de tijd wordt berekend. Volgens het bovenstaande voorbeeld is €1210 de toekomstige waarde van €1000 over twee jaar, vanaf vandaag gerekend.
De equivalente waarde van twee cash flows op twee verschillende tijdstippen wordt soms ook de tijdswaarde van geld genoemd. Door eerder geld te ontvangen, kun je het investeren en later meer geld hebben.
Samengestelde rente is rente over rente, dat wil zeggen dat je in het eerste jaar €100 rente ontvangt, maar in het tweede jaar krijg je €110 aan rente doordat je ook rente krijgt over de al ontvangen rente van het eerste jaar (zie voorbeeld hierboven).
Over het derde jaar ziet de toekomstige waarde er als volgt uit:
€1000 x (1,10) x (1,10) x (1,10) = € 1000 x (1,10)³ = € 1331
In het algemeen ziet de formule voor de toekomstige waarde van een cash flow er als volgt uit:
TWn = C x (1+r) x (1+r) x ……x (1+r) = C x (1+r)ⁿ
Ad 3: terugrekenen van cash flows in de tijd
Stel je wilt de huidige waarde berekenen van € 1000, die je over één jaar ontvangt. De huidige rentevoet bedraagt 10%.
(€1000 over een jaar) ÷ (1,10 € over een jaar / € nú) = € 909,09 nú.
Dus om een cash flow terug in tijd te rekenen, delen wij het door de rentefactor (1 + r), waarbij r de rentevoet is. Dit proces van terugrekenen van een toekomstige cash flow naar de equivalente waarde vandaag, noemen we verdisconteren.
0 jaar 1 jaar 2
——————————————————— Tijdslijn
€826,45 €909,09 €1000
÷ 1,10 ÷ 1,10
Als we de contante waarde van een cash flow van €1000 over drie jaar willen weten, dan doen we dat met de volgende algemene formule:
CW = C(cash flow) ÷ (1 + r)ⁿ = C / (1 + r)ⁿ
Toepassing van regels voor verplaatsing in tijd
Stel we sparen €1000 nú en €1000 aan het eind van elk volgende twee jaren. De bank biedt ons 10% op ons spaartegoed. Hoeveel hebben we na drie jaar gespaard?
0 1 2 3
———————————————————————————— Tijdslijn
€1000 €1000 €1000 ?
Eerst calculeren we de waarde van €1000 dat we nu hebben naar de waarde over een jaar.
0 1 2 3
———————————————————————————— Tijdslijn
€1000 €1000 €1000 ?
→ €1100
x 1,10 -------- +
€2.100
En zo kunnen we de waarde over twee jaar enzovoort berekenen.
0 1 2 3
———————————————————————————— Tijdslijn
€1000 €1000 €1000
→ €1100
x 1,10 -------- +
€2.100
→ €2310
x 1,10 -------- +
€3.310
→ €3.641
x 1.10
Het totale bedrag dat we na drie jaar bij de bank hebben opgebouwd is €3.641.
Wanneer je besluit om €1000 op de bank te zetten voor 20 jaar tegen een rente van 10%. Hoeveel geld heb je dan over 20 jaar?
We gebruiken de formule voor de toekomstige waarde van een cash flow:
€ 1000 x 1,10²º = € 6.727,50
De rente die je in het 21ste jaar krijgt is 10% van € 6.727,50 = € 672,75.
Na 20 jaar is het geld meer dan verzesvoudigd.
Wat gebeurt er met het geld als je het 40 jaar laat staan?
€1000 x 1,40º = €1000 x 1,10²º x 1,10²º = € 45.259,26.
Omdat er rente betaald wordt over al ontvangen rente in het verleden, is de groei van de cash flow exponentieel te noemen.
4.3 Waarderen van een cash flow stroom
Het berekenen van de contante waarde van een cash flow stroom doen we in twee stappen:
bereken de contante waarde van elke individuele cash flow
als alle cash flows in algemene eenheden van euro’s zijn, kunnen we ze combineren.
De tijdslijn voor een gegeven rentevoet r ziet er als volgt uit:
0 1 2 N
————————————————————— - - - - - - - - —— Tijdslijn
C0 C1 C2 Cn
C1/(1+r) ÷ (1+r)
C2/(1+r)² ÷ (1+r)²
Cn/(1+r)ⁿ ÷ (1+r)ⁿ
-------------+
C0 + C1 / (1+r) + C2 / (1+r)² + ……+Cn / (1+r)ⁿ
Deze formule kunnen we ook als een sommatie opschrijven:
De contante waarde van een cash flow stroom is:
n n
CW = ∑ CW ( Cn ) = ∑ Cn / (1 + r)ⁿ
n=0 n=0
De toekomstige waarde op datum n voor een cash flow stroom met een contante waarde van CW is:
TWn = CW x (1+ r)ⁿ
4.4 De netto contante waarde van een cash flow stroom
Nu gaan we kijken naar ons eigenlijke doel, namelijk het berekenen van de netto contante waarde van toekomstige cash flows om een investeringsbeslissing te kunnen evalueren. We hebben al gezien dat de netto contante waarde gedefinieerd wordt als:
NCW = CW (baten) – CW (kosten).
De netto contante waarde van een mogelijke investering is ook de contante waarde van de cash flow stroom van de investeringsmogelijkheid:
NCW = CW (baten) – CW (kosten) = CW (baten – kosten)
4.5 Perpetuïteiten, Annuïteiten en andere speciale gevallen
In deze paragraaf gaan we kijken naar twee soorten activa namelijk:
perpetuïteiten
annuïteiten
Perpetuïteiten
Een perpetuïteit is een stroom van gelijke cash flows, die voorkomen op regelmatige intervallen en eeuwig duren.
Stel: we investeren een bedrag P bij de bank. Elk jaar kunnen we de verdiende rente opnemen.
C = r x P, waarbij bedrag P op de bank blijft. De contante waarde van het ontvangen van cash flow C in een perpetuïteit is daarom de vooraf te betalen kosten:
P = C / r, dus de contante waarde van een perpetuïteit is:
CW ( C in perpetuïteit) = C / r
Door het op de bank zetten van het bedrag C/r nú, kunnen we (C/r) x r = C elke periode in perpetuïteit aan rente ontvangen.
Annuïteiten
Een annuïteit is een stroom van N gelijke cash flows, die op regelmatige intervallen betaald worden.
Het verschil tussen een annuïteit en een perpetuïteit is dat een annuïteit eindigt na een vast aantal betalingen; een perpetuïteit duurt eeuwig.
Stel: we investeren €100 bij de bank tegen 5% rentevoet. Aan het eind van het jaar hebben we €105 bij de bank staan. We nemen ieder jaar de verdiende rente op en laten €100 bij de bank staan.
Bij de perpetuïteit was het principe dat wij het eeuwig blijven doen. Maar bij een annuïteit kun je dat voor een vaste periode van bijvoorbeeld 20 jaar doen.
Met onze initiële investering van €100 hebben wij een 20 jarige annuïteit van €5 per jaar gecreëerd, plus we krijgen nog €100 aan het einde van het 20ste jaar.
€100 = CW (20 jaar annuïteit van €5 p.j.) + CW (€100 over 20 jaar) =
CW (20 jaar annuïteit van € p.j.) = €100 – CW (€100 over 20 jaar) =
= 100 – 100 / (1,05)²º = € 62,31
Dus de contante waarde van €5 voor 20 jaar is €62,31.
Uit het bovenstaande kunnen we de algemene formule afleiden waarbij P de totale contante waarde van twee soorten cash flows is:
P = CW(annuïteit van C voor N periodes) + CW(P in periode N).
Als we deze vergelijking oplossen dan kunnen we de contante waarde van de annuïteit berekenen:
CW(annuïteit van C voor N periodes) = P – CW(P in periode N) =
→ P – P / (1 + r)ⁿ = P ( 1 – (1/(1+r)ⁿ).
We weten dat C = r x P, dus als we P oplossen dan krijgen we:
P = C / r
Als we P oplossen met behulp van de bovenstaande vergelijking, dan krijgen we de formule voor de contante waarde van de annuïteit van C voor N periodes.
CW(annuïteit van C voor N periodes met r) = C x 1/r (1 - (1 / (1+r)ⁿ))
Nu kunnen we ook de formule voor de toekomstige waarde van een annuïteit herleiden. Als we de waarde van N jaren in de toekomst willen weten, moeten we de contante waarde N periodes vooruit in tijd verplaatsen, dat wil zeggen dat we de contante waarde verdisconteren voor N periodes tegen een rentevoet r:
TW(annuïteit) = CW x (1 + r) =
= C / r (1-1/(1+r)ⁿ) x (1 + r)ⁿ =
= C x 1/r ((1+r)ⁿ - 1)
Met deze formule kunnen we bepalen hoeveel een spaarbedrag zal groeien met de tijd.
Groeiende cash flows
Een groeiende perpetuïteit is een stroom van cash flows, die op regelmatige tijdstippen betaald worden en eeuwig groeien met een constante factor.
Stel: een groeiende perpetuïteit met een eerste betaling van €100 die groeit met een rentevoet van 3% heeft de volgende tijdslijn:
0 1 2 3 4
—————————————————————————————- - - -
€ 100 €100x1,03=€103
€103x1,03=€106,09 €106,09x1,03=€109,27
In het algemeen kunnen we stellen dat de tijdslijn van een groeiende perpetuïteit er als volgt uitziet:
0 1 2 3 4
————————————————————————————- - - -
C C x (1+g) C x (1+g)² C x (1+g)³
De formule voor de contante waarde van een groeiende perpetuïteit is:
CW (groeiende perpetuïteit) = C / (r – g) waarbij:
r = rentevoet
g = groeipercentage
C = cash flow (inleg)
Groeiende annuïteit
Een groeiende annuïteit is een stroom van N groeiende cash flows, die op regelmatige intervallen betaald worden.
De tijdslijn van een groeiende annuïteit met een initiële cash flow C, en met een groeipercentage van g voor elke periode tot periode N ziet er als volgt uit:
0 1 2 N
—————————————————- - - - - - - ————
C C(1+g) C(1+g)ⁿ¹
De formule voor de contante waarde van een groeiannuïteit is:
CW = C x 1/(r – g) (1 – ((1+g)/(1+r))ⁿ)
4.6 Oplossen van problemen met spreadsheetprogramma’s
In Excel heb je een aantal functies dat de berekeningen uitvoert, die financiële professionals vaak nodig hebben. Deze functies in Excel heten: NPER, RATE, PV (=CW), PMT en FV (=TW).
Al deze functies zijn gebaseerd op de tijdslijn van een annuïteit:
0 1 2 NPER
—————————————————- - - - - - - —————
PV PMT PMT PMT + FV
4.7 Oplossen van variabelen anders dan CW of TW
Tot nu toe hebben we de contante waarde van de toekomstige waarde van een cash flow stroom berekend. Soms weten we de contante waarde of de toekomstige waarde al, maar we weten niet één van de variabelen die we als input moeten gebruiken.
Oplossen van de cash flow
Stel: we weten de contante waarde van een investering maar we weten niet de cash flows. Als voorbeeld kunnen we denken aan een lening, want we weten hoeveel we moeten lenen (contante waarde) en we kennen de rentevoet, maar we weten niet hoeveel we ieder jaar moeten terugbetalen.
We gaan uit van een initiële investering van €100.000, die we in gelijke jaarlijkse termijnen moeten terugbetalen tegen een rentevoet van 8%.
Wat is de jaarlijkse betaling? Eerst tekenen we een tijdslijn:
0 1 2 10
—————————————————- - - - - - - ————
- €100.000 C C C
100.000 = CW (10 jarige annuïteit van C per jaar, geëvalueerd tegen de leningsrente)
Als we de formule voor de contante waarde van een annuïteit toepassen:
100.000 = C x 1/0,08 ( 1 – 1/1,08¹º) = C x 6,71
• C = 100.000 / 6,71 = €14.903
We moeten dus 10 jaarlijkse betalingen van €14.903 doen in ruil voor €100.000 nú.
De algemene formule voor een periodieke betaling op een lening van N periodes met een geleend bedrag P en een rentevoet r is:
C = P / 1/r (1 – 1/(1+r)ⁿ)
Interne opbrengstvoet
In sommige situaties ken je de contante waarde en de cash flows van een mogelijke investering, maar je weet de rentevoet niet. Deze rentevoet noemen we de interne opbrengstvoet (IRR), dat is de rentevoet die de netto contante waarde van de cash flows gelijk stelt aan nul.
Stel: een mogelijke investering vereist €1000 nú en zal over zes jaar €2000 opleveren. De tijdslijn ziet er als volgt uit:
0 1 2 6
—————————————————- - - - - - - ————
- €1000 €2000
Welke rentevoet r heb je nodig zodat de netto contante waarde van deze investering nul is.
NCW = - 1000 + 2000 / (1+r)⁶ = 0
→ 1000 x (1+r) = 2000 →
→ 1 + r = (2000 / 1000)¹̷ ⁶ = 1,1225
→ r = 12,24%
Het oplossen van het aantal periodes N
In sommige gevallen kennen we de rentevoet, de contante waarde en de toekomstige waarde. Maar nu moeten we berekenen, hoe lang het zal duren voor de contante waarde om te groeien tot de toekomstige waarde (dus we berekenen N).
Stel: we zetten €10.000 bij de bank tegen 10% rentevoet en we willen weten hoe lang het zal duren totdat het bedrag gegroeid is tot €20.000. Als eerste tekenen we de tijdslijn:
0 1 2 N
—————————————————- - - - - - - ————
- €10000 €20000
We willen N berekenen, dus moeten we N zoeken zodat de toekomstige waarde van onze investering gelijk is aan €20.000:
TW = €10.000 x 1,10ⁿ = €20.000
Als we beide zijden van de vergelijking met €10.000 delen dan krijgen we:
1,10ⁿ = 20.000 / 10.000 = 2
Om de exponent N te vinden, moeten we de logaritme van beide zijden nemen en uitgaan van ln (xª) = a ln (x):
N ln (1,10) = ln (2) →
→ N = ln (2) / ln (1,10) = 0,6931 / 0,0953 = 7,3 jaar
Hoofdstuk 5: De rentevoet
Tot nu toe hebben we gekeken naar de technieken voor het berekenen van de contante waarde en de toekomstige waarde, gegeven een markt rentevoet. Maar hoe wordt de rentevoet eigenlijk vastgesteld?
5.1 Rentevoet quote en aanpassingen
Er zijn verschillende manieren waarop de rentevoet genoteerd wordt. Rentevoeten worden vaak genoteerd voor verschillende tijdsintervallen, zoals maandelijks, halfjaarlijks of jaarlijks. Daarom is het noodzakelijk om de rentevoet aan te passen aan een tijdsperiode dat past bij onze cash flow.
De effectieve jaarrente
Rentevoeten worden vaak aangeduid als een effectieve jaarrente (EAR). De effectieve jaarrente geeft het totale bedrag aan rente aan, dat verdiend zal worden aan het eind van een jaar.
Stel: met een EAR van 5% zal een investering van €100.000 groeien tot:
€100.000 x (1 +r ) = €100.000 x (1,05) = €105.000
Over twee jaar zal onze investering van €100.000 groeien tot:
€100.000 x (1 + r)² = €100.000 x (1,05)² = €110.250
Aanpassen van de disconteringsvoet aan verschillende tijdsperioden
De EAR kan gebruikt worden als een verdisconteringsvoet voor jaarlijkse cash flows.
In het algemeen kunnen we met behulp van de onderstaande formule een verdisconteringsvoet r converteren naar een periode, equivalent aan de verdisconteringsvoet voor n periodes:
Equivalent n-periode verdisconteringsvoet = (1 + r)ⁿ - 1
Stel: het verdienen van een effectieve jaarrente van 5% voor twee jaar is equivalent aan het verdienen van 10,25% aan totale rente, over de gehele periode:
€100.000 x (1,05)² = €100.000 x 1,1025 = €110.250
De jaarlijkse percentages
Banken noteren rentevoeten in termen van een jaarlijks percentage (APR).
Een jaarlijks percentage geeft het totale bedrag aan eenvoudige rente over een jaar aan, dat wil zeggen het bedrag aan verdiende rente, zonder het effect van verdiscontering.
Om het eigenlijke bedrag dat je over een jaar zult ontvangen te berekenen, moeten we de APR eerst omrekenen naar een effectieve jaarrente. APR’s kunnen niet gebruikt worden als verdisconteringsvoet, omdat APR’s niet het echte bedrag reflecteren dat je over een jaar zult verdienen.
Daarom moeten we het samengestelde interval, a, van een APR kennen om de EAR vast te kunnen stellen.
Omrekenen van APR naar EAR:
1 + EAR = (1 + APR/a)ª
In onderstaande tabel laten we de effectieve jaarrente van 6% APR zien, met verschillende samengestelde periodes. We moeten opmerken dat gegeven een APR, de EAR zal stijgen met de samengestelde frequentie.
Effectieve jaarrente voor een 6% APR met verschillende samengestelde periodes | ||
Samengesteld interval (a) | Effectieve Jaarrente | |
Jaarlijks | (1 + 0,06 / 1)¹ -1 = | 6% |
Halfjaarlijks | (1 + 0,06 / 2)² - 1 = | 6,09% |
Maandelijks | (1 + 0,06 / 12)¹² - 1 = | 6,1678% |
Dagelijks | (1 + 0,06 / 365)³⁶⁵ - 1 = | 6,1831% |
5.2 Toepassing: verdisconteringsvoet en leningen
Nu we weten hoe je de verdisconteringsvoet met behulp van een rentevoet quote kan berekenen, gaan we dit concept toepassen op twee alledaagse financiële problemen:
berekenen van de periodebetaling van een lening
berekenen van het resterende saldo van een lening
Ad 1: Om de periodebetalingen van een lening te kunnen berekenen, moeten we eerst de verdisconteringsvoet uit de rentevoet quote van de lening herleiden. Daarna kunnen we het saldo van de uitstaande lening gelijkstellen aan de contante waarde van de periodebetalingen van de lening en dit oplossen voor de periodebetalingen.
Een lening met afschrijving is een lening waarbij je elke maand rente over de lening betaalt, plus een deel van het saldo van de lening. Elke betaling is dezelfde en de lening wordt volledig afbetaald met de laatste periodebetaling.
Stel: we hebben een autolening afgesloten. De lening bedraagt €30.000 en zal in 60 maandelijkse betalingen terugbetaald worden tegen 6,75% APR met maandelijkse samengestelde rente.
Als eerste tekenen we de tijdslijn:
0 1 2 60 maanden
—————————————————- - - - - - - ————
€30.000 -C -C -C
De periodebetaling C, moeten we zodanig vaststellen dat de contante waarde van de cash flows, gebruikmakend van de leningsrente, gelijk is aan het oorspronkelijke bedrag van €30.000. Dus 6,75% APR met een maandelijkse samengestelde rente correspondeert met een één-maandelijkse verdisconteringsvoet van 6,75% / 12 = 0,5625%
Omdat de periodebetalingen een annuïteit zijn, kunnen we de volgende formule gebruiken voor het vinden van C:
C = P / 1/r (1 – 1/(1+r)ⁿ) = 30.000 / 1/0,005625 (1 – 1/(1+0,005625)⁶⁰) = € 590,50
Ad 2: Het uitstaande saldo van een lening is gelijk aan de contante waarde van de resterende toekomstige periodebetalingen, gebruikmakend van de leningsrente. We berekenen het uitstaande saldo van de lening door het vaststellen van de contante waarde van de resterende periodebetalingen, gebruikmakend van de leningsrente als een verdisconteringsvoet.
5.3 Determinanten van rentetarieven
Hoe worden rentevoeten vastgesteld? Er zijn diverse factoren die invloed uitoefenen op de rentevoet, zoals inflatie, overheidsbeleid en verwachtingen over toekomstige groei.
Inflatie en reële versus nominale rente
De rentevoeten die door de banken en andere financiële instituties genoteerd worden, en die we gebruikt hebben voor het verdisconteren van cash flows, zijn nominale rentes.
Nominale rente geeft de rentevoet aan waarmee jouw geld zal groeien als je het voor een zekere periode investeert.
De reële rente rr, geeft het percentage van de groei van iemands koopkracht aan, ná aanpassing van de inflatie.
Gegeven een nominale rente r, en een inflatiepercentage i, dan is de formule voor de reële rente als volgt:
rr = r – 1 / 1 + i ≈ r – i
Een nominale rente heeft de neiging om met de inflatie te fluctueren. Als het percentage van de inflatie hoog is, dan is een hogere nominale rente nodig om individuen over te halen om te sparen en vice versa.
Als de kosten van een investering vooraf gaan aan de baten, zal een stijging van de rentevoet de NCW van de investering laten dalen.
De Amerikaanse overheid en centrale banken in andere landen gebruiken deze relatie tussen rentevoeten en investeringsprikkelsom de economie te beïnvloeden. Zij kunnen de rentetarieven verlagen om mensen te stimuleren om te investeren als de economie terugloopt. En zij kunnen de rentetarieven verhogen om investeringen te verlagen als de economie overspannen is en de inflatie toeneemt.
De rendementscurve en de disconteringsvoet
De relatie tussen de investeringstermijn en de rentevoet noemen we de termijnstructuur van de rentevoet. Deze relatie kan in een grafiek weergegeven worden en heet een rendementscurve.
In principe zouden cash flows verdisconteerd moeten worden tegen de disconteringsvoet, die toepasselijk is voor hun investeringshorizon. Vandaar dat de contante waarde van een cash flow stroom, gebruikmakend van een termijnstructuur van de disconteringsvoet er als volgt wordt berekend:
n
CW = (Cn/1+r ) + Cn/(1+r)² + ----------- Cn/ (1+rn)ⁿ = ∑ Cn / (1 + rn)ⁿ
n=1
rn = risicovrije rentevoet voor een n-jarige termijn.
Cn = risicovrije cash flow ontvangen in n jaar.
We moeten opmerken dat de formules voor annuïteiten en perpetuiteïten niet toegepast kunnen worden wanneer de verdisconteringsvoeten variëren met de horizon van de investering.
Rendementscurve en de economie
De helling van de rendementscurve zal sterk beïnvloed worden door de verwachtingen over de rentevoet.
Een sterk stijgende (steile) rendementscurve met lange termijn rentevoeten, die veel hoger zijn dan de korte termijn rentevoeten, geeft in het algemeen aan dat de rentevoeten in de toekomst waarschijnlijk zullen stijgen.
Een dalende rendementscurve met lange termijn rentevoeten, die lager zijn dan korte termijn rentevoeten geeft in het algemeen een verwachte daling van de rentevoeten in de toekomst aan.
De rendementscurve heeft de neiging steil te zijn als de economie uit een recessie komt en verwacht wordt dat de rentevoeten zullen stijgen.
5.4 Risico en belastingen
Bij het evalueren van rentevoeten zijn risico en belastingen belangrijke factoren om rekening mee te houden. Rentevoeten variëren met de termijn van de investering. Rentevoeten variëren ook op basis van de identiteit van degene die leent (risicogevoelig of niet).
De laagste rentekoersen worden betaald op de U.S. Treasuries van de Amerikaanse overheid, aangezien deze risicovrij zijn. Alle andere leners hebben enig risico van in gebreke blijven. Voor deze leningen is de opgegeven rentevoet, het maximumbedrag dat investeerders zullen ontvangen.
Investeerders zullen minder ontvangen als het bedrijf financiële problemen heeft en niet in staat is om de lening volledig terug te betalen. Om dit risico te compenseren dat zij minder ontvangen als het bedrijf in gebreke blijft, vragen investeerders een hogere rentevoet dan de rente op U.S. Treasuries.
We moeten opmerken dat bij het disconteren van toekomstige cash flows, het belangrijk is om een disconteringsvoet te gebruiken die past bij zowel de termijn als het risico van de cash flows.
De juiste verdisconteringsvoet voor een cash flow is het verwachte rendement dat beschikbaar is op de markt op andere investeringen met vergelijkbaar risico en termijn.
Rente na belasting
Belastingen verlagen het rentebedrag dat de investeerder uiteindelijk overhoudt van zijn cash flows. Dit noemen we rente ná belasting.
Stel: een investering levert 8% rente (EAR) op, over een termijn van een jaar. Als je €100 aan het begin van het jaar investeert, dan zal je 8% x €100 = € 8 aan rente verdienen aan het eind van het jaar. Stel dat je 40% belasting moet betalen over deze rente-inkomsten:
(40% inkomstenbelasting) x (€8 rente ) = €3,20 belasting verschuldigd.
Dus je houdt €8 - €3,20 = €4,80 over nadat belastingen zijn betaald.
Dit bedrag is equivalent aan het verdienen van 4,80% rente en géén belasting betalen, dus is de rente na belasting 4,80%.
In het algemeen kunnen we stellen dat als de rentevoet r is en het belastingtarief τ is, dan zal je voor elke €1,00 die je investeert, rente ontvangen gelijk aan r. En je bent belasting verschuldigd over τ x r op de rente.
De algemene formule voor rente ná belasting is:
r – (τ x r) = r (1 – τ)
Als we deze formule toepassen op ons voorbeeld hierboven, dan krijgen we de volgende uitkomst:
8% x (1 – 0,40) = 4,80% rente ná belasting.
Dezelfde berekening geldt ook voor leningen. In sommige gevallen is de rente op een lening aftrekbaar van de belasting. Het netto effect is dat de effectieve rente na belasting gelijk is aan:
r (1 – τ).
Dit betekent dat de mogelijkheid om rente-uitgaven af te kunnen trekken, de effectieve rente ná belasting verlaagt (die op de lening betaald wordt).
5.5 De opportunity kosten van kapitaal
Verder in dit boek zullen we ons baseren op de verdisconteringsvoet, die we gebruiken om cash flows te evalueren op de opportunity kosten van het kapitaal van de investeerder.
Opportunity kosten van het kapitaal is het best beschikbaar verwacht rendement, dat aangeboden wordt op een markt op een investering van vergelijkbaar risico en termijn, op de cash flow die verdisconteerd wordt.
Hoofdstuk 6: Investeringsbeslissingregels
Een bedrijf moet alleen tot acquisitie overgaan als het een positieve netto contante waarde heeft. Hoewel de NCW investeringsregel de waarde van het bedrijf maximaliseert, gebruiken sommige bedrijven echter andere technieken om investeringen te evalueren en te beslissen met welke projecten ze zich moeten bezighouden.
6.1 NCW en alleenstaande projecten
De NCW regel
Stel: een bedrijf, FFF, heeft een nieuwe milieuvriendelijke meststof ontwikkeld, dat zij tegen substantiële kosten kan produceren met besparing op de bestaande productlijn van het bedrijf. Deze meststof heeft een nieuwe installatie nodig, die meteen gebouwd kan worden tegen €250 miljoen. De baten van deze nieuwe meststof zullen naar verwachting €25 miljoen per jaar bedragen, aanvangend bij het einde van het jaar en zullen eeuwig duren.
0 1 2 3 4
————————————————————————————- - - -
-€250 €35 €35 €35 €35
De NCW van deze cash flow stroom, gegeven een disconteringsvoet r is:
NCW = - 250 + 35/r
We kunnen de NCW als een functie van de disconteringsvoet weergeven in een grafiek.
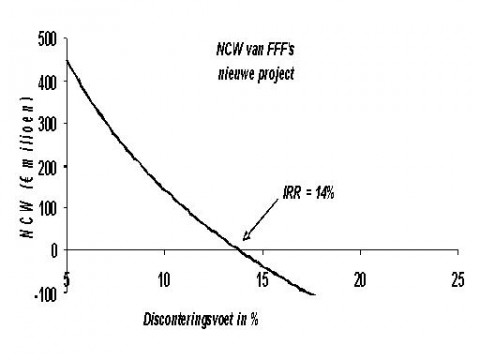
De NCW is positief voor alle verdisconteringsvoeten die kleiner zijn dan 14%, de IRR. Om te kunnen besluiten of we moeten investeren (NCW regel), moeten we de kosten van kapitaal weten. De managers die verantwoordelijk zijn voor dit project, schatten de kosten van kapitaal op 10 % per jaar. In de grafiek zien we dat als de verdisconteringsvoet 10% is, de NCW €100 miljoen zal zijn en dat is positief.
De NCW investeringsregel stelt dat door deze investering de waarde van het bedrijf zal stijgen met €100 miljoen, dus moet FFF dit project aannemen.
Meten van gevoeligheid met de IRR
Stel: als de geschatte kosten van kapitaal meer dan 14% IRR bedragen, dan zal de NCW negatief zijn.
In het algemeen kunnen we stellen dat het verschil tussen de kosten van het kapitaal en de IRR, is het maximale bedrag van een schattingsfout in de verwachte schatting van de kosten van kapitaal, die kan bestaan zonder het veranderen van de oorspronkelijke beslissing.
Alternatieve regels versus de NCW regel
Een positieve NCW leidt tot het maximaliseren van de welvaart. Als wij het project op basis van andere regels dan de NCW regel aannemen, dan leidt dat tot een verkeerd besluit en de welvaart wordt dan niet gemaximaliseerd.
6.2 De interne opbrengstvoet regel (IRR)
De IRR investeringsregel zegt dat als de investeringsmogelijkheid die je overweegt, groter is dan het rendement op andere alternatieven in de markt met equivalent risico en kosten van het kapitaal, moet je de investering goedkeuren.
De IRR investeringsregel: neem elke investeringsmogelijkheid waarbij de IRR de opportunity kosten van het kapitaal overschrijdt. Keur elke investeringskans af als de IRR lager is dan de opportunity kosten van het kapitaal.
In het algemeen werkt de IRR regel voor een alleenstaand project als alle negatieve cash flows van het project worden voorafgegaan aan haar positieve cash flows. Anders zal de IRR regel niet overeenkomen met de NCW regel en zal de uitkomst incorrect zijn.
De IRR regel kan dus een verkeerd antwoord geven als de cashflows een vooraf betaling hebben (negatieve investering). De IRR regel kan ook niet gebruikt worden als er sprake is van meerdere IRR’s of als de IRR niet bestaat. In dit soort gevallen kunnen we alleen vertrouwen op de NCW regel.
6.3 De terugbetalingsregel
De eenvoudigste investeringsregel is de terugbetalingregel, die gebaseerd is op het idee dat als een mogelijke investering haar initiële kosten snel terugverdient, dan is het een goede investering.
De terugbetalingregel: bereken het bedrag in tijd dat nodig is om de initiële investering terug te betalen (= terugbetalingperiode).Als de terugbetalingperiode korter is dan de vooraf vastgestelde lengte in tijd, accepteer het project. Anders moet je het afwijzen.
Stel: het bedrijf FFF vereist dat alle projecten een terugbetalingperiode hebben van vijf jaar of korter. Zou het bedrijf het meststofproject aannemen als deze regel geldt?
De som van de cash flows van jaar één tot en met jaar vijf is:
€35 x 5 = €175 miljoen
Dit bedrag zal de initiële investering van €250 miljoen niet dekken. Omdat de terugbetalingperiode voor dit project meer dan vijf jaar bedraagt, zal FFF dit project afwijzen.
De terugbetalingregel is niet betrouwbaar omdat het de tijdswaarde van geld negeert en niet afhangt van de kosten van kapitaal.
6.4 Wederzijds exclusieve investeringen
Tot nu toe hebben we gekeken naar een enkel project waarbij je de keuze had tussen afwijzen of accepteren. Wanneer projecten zoals een marktcampagne wederzijds exclusief zijn, is het niet genoeg om slechts vast te stellen welke projecten een positieve NCW hebben.
Met wederzijds exclusieve projecten is het doel van de manager de projecten te rangschikken en daaruit de beste te kiezen.
In dit geval geeft de NCW regel een eenvoudig antwoord:
kies het project met de hoogste NCW.
Aangezien de IRR een maatstaf is van het verwachte rendement van de investering, kun je niet kiezen voor het project met de hoogste IRR. Dit kan tot verkeerde beslissingen leiden omdat wederzijds exclusieve investeringen verschillende schalen hebben (vereisen verschillende initiële investeringen), of als ze verschillende cash flow patronen hebben.
Verschillen in schaal
Als een project een positieve NCW heeft dan kunnen we, indien mogelijk, de omvang ervan verdubbelen waardoor de NCW ook zal verdubbelen.
Echter, de IRR regel heeft deze eigenschap niet. Het blijft ongewijzigd door de schaal van de investeringskans omdat de IRR een maatstaf is voor het gemiddelde rendement op de investering. Dus kan de IRR regel niet gebruikt worden om projecten met elkaar te vergelijken, die een verschillende schaal hebben.
Voorbeeld identieke schaal
Stel: we hebben twee wederzijds exclusieve projecten met dezelfde schaal. Don overweegt twee investeringsmogelijkheden. Hij kan met zijn vriendin een zaak beginnen, dan kost het hem €1000 en de opbrengsten zijn incrementele cash flows van €1100 per jaar, en eeuwig dalend met 10%.
Het alternatief is dat hij een wasserette met één wasmachine kan beginnen. De was/droogautomaat kost €1000 in totaal en zal €400 per dag genereren, maar dat zal uiteindelijk dalen naar 20% per jaar wegens onderhoudskosten. De opportunity kosten van het kapitaal voor beide investeringsmogelijkheden zijn 12% en beiden vereisen alle tijd van Don, dus moet hij één van de twee kiezen. Welke investering moet hij kiezen?
De tijdslijn voor de investering van een zaak met zijn vriendin ziet er als volgt uit:
0 1 2 3
—————————————————————————- - - -
-€1000 €1100 €1100(1-0,1) €1100(1-0,1)²
De toekomstige cash flows zijn een perpetuïteit met een groeipercentage van -10%, dus de NCW van de investeringsmogelijkheden, als r = 12%, is:
NCW = -1000 +1100/r+0,1 = -1000 + 1100/0,12+0,1 = €4.000
We kunnen de IRR van deze investering berekenen door de NCW gelijk te stellen aan nul en dan oplossen voor r:
1000 = 1100/r+0,1 r = 100%
Deze uitkomst wil zeggen, dat de IRR voor Don’s investering in een zaak met zijn vriendin is gelijk aan 100%.
Nu gaan we naar de tweede mogelijkheid kijken namelijk, de wasserette. De tijdslijn hiervoor is:
0 1 2 3
—————————————————————————- - - -
-€1000 €400 €400(1-0,2) €400(1-0,2)²
Ook nu zijn de toekomstige cash flows een perpetuïteit, maar nu met een negatief groeipercentage van -20%. De NCW van de wasserette-investering is:
NCW= -1000 + 400/r=0,2 = -1000 + 400/0,12+0,2 = €250
De €250 NCW van de wasserette is lager dan de €400 NCW van de investering in de zaak met zijn vriendin samen. Dus moet hij voor de investering in de zaak met zijn vriendin kiezen.
Verandering in schaal
Wat gebeurt er als we de schaal van één van beide projecten veranderen.
Stel: aangezien Don voldoende ruimte heeft in de wasserette, kan hij makkelijk twintig machines plaatsen in plaats van één. Wat moet Don doen?
We moeten opmerken dat de IRR niet beïnvloed wordt door de schaal.
Een wasserette met twintig machines heeft exact dezelfde IRR als een wasserette met slechts één machine. Dus de IRR van een zaak met zijn vriendin is nog steeds hoger dan die van de wasserette.
Echter de NCW van de wasserette groeit door de verandering in schaal: het wordt twintig keer hoger.
NCW = 20( -1000 + 400/(0,12+0,2)) = €5.000
Nu moet Don investeren in de wasserette met twintig machines. De onderstaande grafiek laat de NCW van beide mogelijkheden zien.
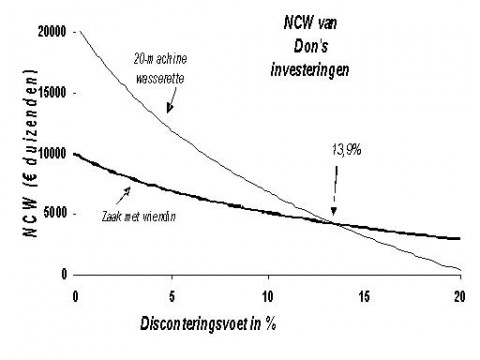
De NCW van de wasserette met twintig machines overschrijdt de NCW van de investering in de zaak met zijn vriendin samen, voor alle gevallen waarbij de kosten van het kapitaal lager zijn dan 13,9% (zie grafiek). Hoewel de IRR van de investering met zijn vriendin hoger is dan die van de wasserette, zal het kiezen van de investering met de hoogste IRR niet dezelfde uitkomst geven als het kiezen van de investering met de hoogste NCW.
Procentueel rendement versus waarde in euro’s
Het lijkt vreemd dat iemand een investering met 100% rendement (IRR) afwijst voor 20% rendement. Dit komt doordat de laatste investering meer geld oplevert.
Stel: we hebben twee investeringsalternatieven:
je kunt 200% rendement verdienen op €1,00 of
je kunt 10% rendement verdienen op €1miljoen.
De eerste investering lijkt veel, maar levert slechts €2,00 op. De tweede investering lijkt weinig, maar levert €100.000 op. De IRR meet het gemiddelde rendement. Wanneer je wederzijds exclusieve projecten vergelijkt met verschillende schalen, moet je de impact van de euro op de waarde van de investering weten, ofwel de NCW.
De duur van de cash flow
Een ander probleem met de IRR is dat het gewijzigd kan worden door het veranderen van de duur van de cash flows, zelfs als deze verandering in tijd geen invloed heeft op de NCW. Daarom is het mogelijk om de rangschikking van de IRR’s van projecten te wijzigen, zonder de rangschikking in termen van de NCW te veranderen. Vandaar dat je de IRR niet kan gebruiken om te kiezen tussen wederzijds exclusieve investeringen.
De incrementele IRR regel
De incrementele IRR investeringsregel past de IRR regel toe op het verschil tussen de cash flows van twee wederzijds exclusieve alternatieven.
Stel: je vergelijkt twee wederzijds exclusieve investeringen A en B. De IRR’s van beide mogelijkheden overschrijden de kosten van kapitaal. Als je de cash flows van B aftrekt van de cash flows van A, dan moet je kiezen voor A als de incrementele IRR de kosten van kapitaal overschrijdt. Anders moet je voor B kiezen.
Toepassing van de incrementele IRR regel
Stel: Don kan een onderhoudscontract nemen, waarbij hij €250 per jaar aan onderhoud voor iedere machine moet betalen. Door dit contract hoeft hij niet zelf voor onderhoud van zijn machines te betalen en zal de cash flow van de machines niet dalen. De verwachte cash flows worden dan:
€400 - €250 = €150 per jaar per machine, voor eeuwig.
Nu passen we de incrementele IRR regel toe. Eerst tekenen we de tijdslijn voor dit project:
0 1 2 3 4 Jaar
————————————————————————————- - - -
- €1000 €150 €150 €150 €150 Met contract
- €1000 €400 €400(0,8) €400(0,8)² €400(0,8)³ Zonder contract
€ 0 - €250 - €170 - €106 - €55 Incrementele cash flows
De NCW van de incrementele cash flow is het verschil tussen NCW met contract en NCW zonder contract:
NCW = 150/r – 400/r+0,2
Als we deze vergelijking gelijkstellen aan nul en oplossen voor r, dan krijgen we een IRR van 12%. Volgens de incrementele regel moet Don het contract accepteren, wanneer de kosten van het kapitaal lager zijn dan 12%. Omdat zijn kosten van kapitaal in dit voorbeeld gelijk zijn aan 12%, is hij indifferent.
Tekortkomingen van de incrementele IRR regel
De incrementele IRR heeft net als de gewone IRR ook te maken met een aantal problemen namelijk,
het feit dat de IRR de kosten van kapitaal van beide projecten overschrijdt, houdt niet in dat beide projecten positieve NCW hebben.
de incrementele IRR hoeft niet te bestaan.
er kunnen meerdere IRR’s bestaan.
je moet in de gaten houden welk project het incrementele project is en ervan verzekerd zijn dat de incrementele cash flows in het begin negatief zijn en dan positief worden. Anders zal de incrementele IRR regel het probleem hebben van een negatieve initiële investeringsprobleem, en dat zal leiden tot een verkeerde uitkomst.
de incrementele IRR regel veronderstelt dat het risico van twee projecten hetzelfde is. Als de risico’s verschillend zijn, dan zijn de kosten van het kapitaal van de incrementele cash flows niet duidelijk. In dit geval kan alleen de NCW regel een betrouwbaar antwoord geven.
Kort samengevat: hoewel de incrementele IRR regel een betrouwbare methode kan zijn bij het kiezen tussen twee projecten, toch kan het moeilijk zijn om het correct toe te passen. Het is veel eenvoudiger om de NCW regel toe te passen.
6.5 Selectie van projecten met beperking van middelen
In sommige gevallen kunnen verschillende investeringsmogelijkheden verschillende bedragen van een bepaalde bron of middel vereisen. Als het aanbod van de bron vast is, kun je niet alle mogelijke investeringen plegen door simpelweg dié mogelijkheid te kiezen met de hoogste NCW. Dit zou niet tot de beste uitkomst kunnen leiden.
Evaluatie van projecten met verschillende bronvereisten
Stel: je overweegt drie projecten uit onderstaand tabel, die alle drie bepaalde ruimte vereisen van het opslagmagazijn.
Mogelijke projecten die magazijnruimte vereisen | |||
Project | NCW (€ miljoen)) | Fractie v. magazijnruimte (%) | Winstgevendheidindex |
A | 100 | 100 | 1 |
B | 75 | 60 | 1,25 |
C | 75 | 40 | 1,875 |
Project A heeft de hoogste NCW maar het gebruikt alle ruimte van het magazijn (bron), dus zou het fout zijn om hiervoor te kiezen. Projecten B en C kunnen allebei geaccepteerd worden (samen gebruiken ze alle beschikbare ruimte), en hun gecombineerde NCW overschrijdt de NCW van project A, dus moet je B en C kiezen. Hun gezamenlijke NCW is €15 n0 miljoen, vergeleken met slechts €100 miljoen van project A alleen.
Winstgevendheidindex
De winstgevendheidindex wordt vaak gebruikt om de optimale combinatie van potentiële projecten te identificeren.
De winstgevendheidindex is:
Winstgevendheidindex = Gecreëerde waarde / geconsumeerde hulpbronnen
= NCW / geconsumeerde hulpbronnen
Nadat we de winstgevendheidindex berekend hebben, kunnen we de projecten op basis daarvan rangschikken. We beginnen met het project met de hoogste index en vervolgens gaan we verder met het rangschikken van alle projecten totdat de hulpbron op is. In bovenstaande tabel kunnen we zien waarom je voor B en C moet kiezen als je gebruik maakt van de winstgevendheidindex.
Tekortkomingen van de winstgevendheidindex
Hoewel de winstgevendheidindex eenvoudig te berekenen en te gebruiken is, geeft het in sommige situaties geen nauwkeurig antwoord.
Een groter probleem ontstaat als er sprake is van meerdere beperkingen van hulpmiddelen, daardoor mislukt de winstgevendheidindex volledig. De enige zekere manier om de beste combinatie van projecten te vinden, is dan om ze allemaal een voor een en met elkaar te onderzoeken.
Hoofdstuk 7: Basis van kapitaal budgettering
Een belangrijke verantwoordelijkheid van de financiële managers van een corporatie is het vaststellen, welke projecten of investeringen een bedrijf moet ondernemen.
Kapitaalbudgettering is het proces van analyseren van de investeringsmogelijkheden en beslissen welke acceptabel zijn. Dit vereist het berekenen van de netto contante waarde en het accepteren van projecten, waarvan de NCW positief is.
De eerste stap in dit proces is het schatten van de verwachte cash flows van het project door het voorspellen van de opbrengsten en kosten van het project. Als we deze cash flows gebruiken, dan kunnen we de NCW van het project berekenen.
7.1 Voorspelling van de inkomsten
Een kapitaalbegroting geeft de projecten en investeringen weer die een bedrijf van plan is te ondernemen gedurende het komende jaar. Om deze lijst vast te stellen moeten bedrijven alternatieve projecten analyseren. Vervolgens beslissen ze welke projecten zij willen accepteren via het proces van kapitaal budgettering.
Ons ultieme doel is het vaststellen van het effect van de beslissing op de cash flows van het bedrijf. De financiële manager begint met het vaststellen van de incrementele inkomsten van een project, dat is het bedrag waarmee de inkomsten van het bedrijf verwacht worden te veranderen als gevolg van de investeringsbeslissing.
Incrementele winstverwachting
Investeringsuitgaven en afschrijvingen: investeringen in fabriek, goederen en uitrusting zijn kasuitgaven. Deze kasuitgaven worden niet direct als uitgaven weergegeven bij het berekenen van de inkomsten. In plaats daarvan trekt het bedrijf ieder jaar een fractie van de kosten van deze onderdelen af als afschrijving.
De simpelste methode hiervoor is de lineaire afschrijving, waarbij de kosten van de activa gelijkmatig verdeeld worden over hun levensduur.
Rente-uitgaven: om het netto-inkomen van een bedrijf te berekenen, moeten we eerst de rente-uitgaven aftrekken van de inkomsten voor rente en belasting (EBIT). Wanneer we een kapitaal budgetteringsbeslissing evalueren, zullen we in het algemeen de rente-uitgaven niet meenemen bij de afweging.
Rente-uitgaven hebben te maken met de financiering van het project, dus wordt dit niet meegenomen bij het beoordelen van het project op zichzelf.
Het netto-inkomen wordt hier de ‘unlevered’ netto-inkomen van het project genoemd om aan te geven dat in dit netto-inkomen geen rente-uitgaven die met de vermogensstructuur te maken hebben, inbegrepen zijn.
Belastingen: we moeten ook rekening houden met de vennootschapsbelasting. Daarvoor gebruiken we het marginale vennootschapsbelastingtarief, dat is het belastingtarief die op een incrementele euro van het inkomen betaald moet worden vóór belastingen.
Stel: het vennootschapsbelastingvoor een project is 40% ieder jaar. De incrementele belastinguitgave wordt dan als volgt berekend:
Inkomstenbelasting = EBIT x tc
tc = het marginale belastingtarief van het bedrijf.
Berekenen van het ‘unlevered’ netto-inkomen: de formule voor het berekenen van het ‘unlevered’ netto-inkomen is:
‘Unlevered’ netto-inkomen = EBIT x (1 - tc) =
= (Opbrengsten – Kosten – Afschrijvingen) x (1 - tc)
Het ‘unlevered’ netto-inkomen van een project is gelijk aan haar incrementele opbrengsten minus de kosten en afschrijvingen, geëvalueerd na aftrek van belastingen.
Indirecte effecten op incrementele inkomsten
De incrementele inkomsten zouden alle incrementele kosten en opbrengsten moeten inhouden die bij het project horen, inclusief de opportunitykosten en externe effecten, maar exclusief gezonken kosten en rente-uitgaven.
Opportunity kosten: veel projecten gebruiken bronnen/middelen die het bedrijf al bezit. Het lijkt dan dat deze bronnen niks kosten. Echter, in veel gevallen kan deze hulpbron voor een ander project waarde opleveren.
Daarom noemen we dit opportunity kosten:
dat is de waarde die een hulpbron kan opleveren als het op een alternatieve manier wordt gebruikt. Omdat deze waarde verloren gaat als de hulpbron voor een ander project wordt gebruikt, zouden we de opportunity kosten moeten opnemen als een incrementele kostenpost van het project.
Externe effecten van het project: dit zijn indirecte effecten van het project die de winst van andere bedrijfsactiviteiten kunnen verhogen of verlagen.
Als de verkoop van een nieuw product, de verkoop van een bestaand product beïnvloedt dan wordt dat kannibalisering genoemd.
Gezonken kosten en incrementele inkomsten
Gezonken kosten zijn onherstelbare kosten waarvoor het bedrijf al aansprakelijk is. Gezonken kosten zullen toch betaald moeten worden onafhankelijk van de beslissing of het project doorgaat of niet. Daarom zijn deze kosten niet incrementeel en worden dus niet meegenomen in de analyse van een project. Een voorbeeld van gezonken kosten zijn overheaduitgaven.
7.2 Het vaststellen van de vrije cash flow en NCW
De inkomsten zijn een boekhoudkundige maatstaf voor het functioneren van het bedrijf. Het geeft namelijk niet het werkelijke rendement weer. Het bedrijf kan de inkomsten gebruiken om goederen te kopen, werknemers te betalen, dividend uitkeren, enzovoort. Daarvoor heeft het bedrijf kasgeld nodig.
Dus om een kapitaalbudgetteringsbeslissing te evalueren, moeten we vaststellen wat de gevolgen zijn voor het beschikbare kasgeld van het bedrijf. Het incrementele effect van een project op het beschikbare geld van het bedrijf noemen we de vrije cash flow.
Het berekenen van de vrije cash flow uit inkomsten
Zoals aangegeven in hoofdstuk twee zijn er belangrijke verschillen tussen inkomsten en cash flows.
Inkomsten bevatten bijvoorbeeld wel afschrijvingen maar niet de kosten van het kapitaal. Daarom moeten we het bedrag van de incrementele inkomsten aanpassen om de vrije cash flow te kunnen berekenen.
Kapitaaluitgaven en afschrijving: omdat een afschrijving niet een cash flow is, zal het niet meegenomen worden in het voorspellen van de cash flow. In plaats daarvan nemen we de werkelijke aanschafkosten van de activa mee in onze voorspelling.
Het netto werkkapitaal: dit is het verschil tussen vlottende activa en kortlopende schulden. De belangrijkste componenten van het netto werkkapitaal zijn: kasgeld, inventaris, vorderingen en schulden.
Netto werkkapitaal = Vlottende activa – Kortlopende schulden
= Kasgeld + Inventaris + Vorderingen – Schulden
Veel projecten zullen vereisen dat het bedrijf investeert in het netto werkkapitaal.
De vorderingen van het bedrijf meten het totale krediet dat het bedrijf heeft uitstaan bij haar klanten.
De schulden van het bedrijf meten het krediet dat het bedrijf heeft ontvangen van haar aanbieders.
Het verschil tussen vorderingen en schulden is het netto kapitaalbedrag van het bedrijf dat gebruikt is als een resultaat van deze krediettransacties, genaamd handelskrediet.
De vrije cash flow wordt dus berekend door de incrementele inkomsten te verminderen met alle ‘niet kasuitgaven’ en te vermeerderen met alle kapitaalinvesteringen:
Afschrijving is geen kasuitgave, dus wordt het erbij opgeteld
Werkelijke kapitaaluitgaven worden afgetrokken
Toename van het netto werkkapitaal wordt ook afgetrokken.
Direct berekenen van de vrije cash flow
De basisformule voor het berekenen van de vrije cash flow is:
Unlevered netto inkomen
Vrije Cash Flow = (Opbrengsten – kosten – Afschrijvingen) x ( 1 - tc) +
+ Afschrijvingen – Kapitaal uitgaven - ∆ Netto werkkapitaal
Dit kunnen we herschrijven als:
Vrije Cash Flow = (Opbrengsten – Kosten) x ( 1 - c) – Kapitaal uitgaven – ∆ Netto werkkapitaal + c x Afschrijvingen
Hierbij geldt dat de stijging van het netto werkkapitaal (NWC) als volgt wordt berekend:
∆ Netto werkkapitaal = NWCt – NWCt-1
De factor c x Afschrijvingen wordt het belastingeffect van afschrijvingen genoemd. Het belastingeffect van afschrijvingen is de belastingbesparing, die het resultaat is van het feit dat afschrijvingen aftrekbaar zijn.
Dus uitgaven aan afschrijvingen hebben een positieve impact op de vrije cash flows.
Berekenen van de NCW
De kosten van het kapitaal van een project kunnen we ook omschrijven als: het verwachte rendement dat de investeerders hadden kunnen verdienen op hun best mogelijk investeringsalternatief met gelijk risico en looptijd.
Om de NCW te berekenen, moeten we de vrije cash flow verdisconteren tegen de bijpassende kosten van het kapitaal.
De contante waarde van de vrije cash flow (FCF) wordt dan:
CW (FCFt) = FCFt / (1+r)ʵ =
= FCFt x 1 / (1+r)ʵ
t-jaar disconteringsfactor
7.3 Kiezen tussen alternatieven
Vaak moeten bedrijven kiezen tussen wederzijds exclusieve alternatieven, waarbij elk alternatief gevolgen heeft voor de cash flow van het bedrijf. In dergelijke gevallen kunnen we eerst de vrije cash flows van ieder alternatief berekenen en dan het alternatief met de hoogste NCW kiezen.
7.4 Verdere aanpassingen van de vrije cash flow
Er kan een aantal complicaties optreden bij de schatting van de vrije cash flow van een project zoals,
overig non-kasgeld items: deze items zouden niet meegerekend moeten worden met de vrije cash flow van het project. Het bedrijf zou alleen werkelijke opbrengsten en uitgaven moeten meerekenen.
duur van de cash flows: cash flows kunnen uitgespreid worden over het hele jaar. We kunnen cash flows schatten per kwartaal, maandelijks of zelfs op een continue basis als grote mate van nauwkeurigheid vereist is.
versnelde afschrijving: omdat afschrijving een positieve bijdrage levert aan de cash flow van het bedrijf door het belastingeffect van de afschrijving, is het in het belang van het bedrijf om de meest versnelde methode van afschrijving te gebruiken die toegestaan is voor belastingdoeleinden.
liquidatie of bergingswaarde: activa die niet meer nodig zijn hebben vaak een wederverkoopwaarde of enige bergingswaarde als de onderdelen verkocht worden aan een sloperij.
Bij het berekenen van de vrije cash flow, wordt ook de liquidatiewaarde van activa meegerekend, die niet meer nodig zijn en verwijderd mogen worden. Als een actief geliquideerd is, zal elke kapitaalverdienste belast worden als inkomen.
De vermogenswinst is het verschil tussen de verkoopprijs en de boekwaarde van het actief.
Dus:
Vermogenswinst = Verkoopprijs – Boekwaarde
De boekwaarde van het actief is:
Boekwaarde = Aanschafprijs – Cumulatieve afschrijvingen
We moeten de vrije cash flow van het project aanpassen om rekening te houden met de cash flow ná belasting, die als gevolg van verkoop van activa als volgt kan ontstaan:
Cash flow na belasting en activa verkoop = Verkoopprijs – (tc x Vermogenswinst)
Beëindiging- of continueringwaarde: soms voorspelt een bedrijf expliciet de vrije cash flow over een kortere horizon dan de volledige horizon van het project of de investering. In dit geval schatten we de resterende waarde van de vrije cash flow verder dan de voorspellingshorizon door het opnemen van een additionele, eenmalige cash flow aan het eind van de voorspellingshorizon genaamd de beëindiging- of continueringwaarde van een project.
Dit bedrag geeft de marktwaarde van de vrije cash flow weer vanaf het project tot alle toekomstige data.
Voorwaarts verrekenen van fiscale verliezen: om te bepalen in welk belastingschaal het bedrijf valt, moet er gekeken worden naar het niveau van het inkomen vóór belasting.
Twee additionele kenmerken van de belastingwetgeving zijn genaamd:
voorwaarts verrekenen van fiscale verliezen (twintig jaar vooruit).
achterwaarts verrekenen van fiscale verliezen (twee jaar terug).
Nederlandse belastingplichtigen voor de vennootschapsbelasting kunnen 9 jaar voorwaarts en 1 jaar achterwaarts hun verliezen verrekenen.
Daarmee wordt bedrijven toegestaan om verliezen gedurende het lopende jaar te compenseren met de inkomsten van de komende jaren.
7.5 Analyseren van het project
Bij het evalueren van een kapitaalbudgetteringsproject moeten financiële managers, dié beslissing nemen, kiezen voor de beslissing die de NCW maximaliseert.
Om de NCW van een project te bepalen, hebben we een schatting van de incrementele cash flows nodig en we moeten een disconteringsvoet kiezen.
Break-even analyse
Indien we onzeker zijn ten aanzien van de input van een kapitaal budgetteringsbeslissing, is het vaak gebruikelijk om het break-even niveau van dat input vast te stellen. Dat is het niveau waarbij de investering een NCW van nul heeft.
Bij de break-even analyse berekenen we voor elke parameter de waarde waarbij de NCW van het project gelijk is aan nul. Daarnaast kunnen we de EBIT break-even voor de verkoop berekenen, dat is het niveau van de verkoop waarbij de EBIT van het project gelijk is aan nul.
Gevoeligheidsanalyse
Een ander kapitaalbudgetteringsinstrument is gevoeligheidsanalyse.
Een gevoeligheidsanalyse hakt de NCW berekening in een aantal veronderstellingen van haar componenten en laat zien hoe de NCW varieert als de onderliggende veronderstellingen veranderen.
Op deze manier maakt een gevoeligheidsanalyse het mogelijk om de effecten van eventuele fouten in de schattingen van de NCW te ontdekken.
Scenario analyse
Tot nu toe hebben we gekeken naar de gevolgen van het variëren van slechts één parameter tegelijk. In werkelijkheid kunnen bepaalde factoren effect hebben op meer dan een parameter.
Scenario analyse beschouwt het effect op de NCW van het veranderen van meerdere parameters van een project.
Join with a free account for more service, or become a member for full access to exclusives and extra support of WorldSupporter >>

JoHo can really use your help! Check out the various student jobs here that match your studies, improve your competencies, strengthen your CV and contribute to a more tolerant world








Add new contribution