Lecture notes with Experimental and Correlational Research at the Leiden University - 2018/2019
Lecture 1
6/2/2019
-Correlation is about two variables being associated, but there is no evidence of causality.
-Causality however requires multiple factors: covariance (variables have an association), directionality(cause precedes effect (in time)) and internal validity(eliminate alternative explanations).
- Correlations can be displayed in scatterplots that show:
- Direction: positive or negative
- Strength: density of the points
- Shape: linear/nonlinear and homogeneous (one cluster) / heterogeneous (multiple clusters).
- Outliers
-Covariance (sxy): to measure the degree to which two variables vary together.
Formula: sxy = Σ(xi-x)(yi-y) / N-1
It provides us with information on the strength and direction of the association. The disadvantage is that the covariance is dependent on the unit of measurement of the variables.
-Pearson r is a standardized measure that describes the linear relationship between two quantitative variables, and always lies between -1 and +1.
Formulas: r = sxy / sxsy Alternative: r = Σzxzy / N-1
- Remember that a z-score is a standardized score that displays how many standard deviations a certain score is away from the mean.
Alternative correlational techniques:
- The Pearson r is the correlation coefficient that is most commonly used. There are alternatives:
quantitative + quantitative --> Pearson r
ordinal + ordinal --> Spearman’s rho (rs)
dichotomous(only two possible values)+ quantitative --> point-biserial correlation (rpb)
dichotomous + dichotomous --> phi coefficient (ϕ)
-Spearman’s rho (rs) describes relationship between two ordinal variables/ranked scores.
Formulas: xrank = N + 1 / 2 srank = √ (N(N+1) / 2)
rs = r on ranked data
Spearman’s rho is also an alternative to Pearson r in case of outliers and/or weak non-linearity.
-Point-biserial correlation describes relationship between quantitative and dichotomous variables. We use the Pearson correlation formula to calculate rpb: rpb = r
The sign of the correlation (+/-) depends on the way 0 and 1 are assigned to groups.
Relationship rpb and tindependent: rpb = Square root of t2 / t2 + df
-Phi-coefficient (ϕ) describes relationship between two dichotomous variables: ϕ = r
There is also a specific formula to calculate ϕ when you make a 2✕2 contingency table:
ϕ = √ (AD - BC / (A+B)(C+D)(A+C)(B+D) )
Relationship ϕ and χ2: ϕ = √(χ2 / N) χ2= ϕ2 ✕ N
- Testing the significance of r, rs, rpb or ϕ: t = r √ N-2 / √1-r2 with df = N - 2.
- Testing the difference between two independent r’s: z = r'1 - r'2 / √ 1/N1-3 + 1/N2-3
Important is to transform r to r’ first, according to Fisher's table.
- Statistical significance depends on N, r and α; so weak correlations in large samples can become significant and strong correlations in small samples might not be significant. So, testing only for significance is too limited.
- Measures of effect size: reffect, r2 (COD, VAF), Cohen’s d or Hedges’s g
- Correlation r is already an effect size; reffect
- The advantage of r2‘s (Coefficient Of Determination; COD, or Proportion of Variance Accounted For; VAF) is that we can compare them. But using r2 also has drawbacks.
- Cohen’s d and Hedges’s g are suitable for comparing the means of two groups (rpb).
Cohen’s d: |μ1 - μ2 | / σ
Hedges’s g: |x1 - x2| / sp
The formulas were especially designed to leave out the size of N (~> comparison to t)
- Rules of thumb:
d/g r r2 rpb r2pb
Small 0.20 0.10 0.01 0.10 0.01
Medium 0.50 0.30 0.09 0.24 0.06
Large 0.80 0.50 0.25 0.37 0.14
Lecture 2
13/2/2019
Simple linear regression:
- Correlations describe linear associations between two (interval) variables.
Regression enables you to estimate one interval variable from one or more others.
- In regression there is a clear distinction between the predictor variable (X) and the response/criterion variable (Y).
- 1 predictor variable --> simple linear regression
2 predictor variables --> multiple linear regression
- (Unstandardized) regression equation: (^ indicates an estimation)
b0= intercept/constant: predicted value of y when x = 0
b1= slope: size of the difference in y^ when x increases by 1 unit
- Error/residual (ei) = the difference between observed (yi) and predicted value (y^i)
Best fit of the data when Σei is minimized.
-b0 = ybar - b1xbar
b1= sxy / s2x = r * sy / sx
-Interpolation is making a prediction within the range of X and Y
Extrapolation is making a prediction outside the range of X and Y
- Problem; when the unit of measurement changes, regression equations change as well. So we use standardized regression equations: zbary = rzx
Accuracy of prediction:
- How good is the model: Our data consist of explained data and some error/unexplained data. Best fit of the data when Σei2 is minimized
- Total variance: SStotal / dftotal Σ(yhat-ybar)2 / N-1 (N-1 are the degrees of freedom of y)
Model variance: SSmodel/ dfmodel Σ(yhat-ybar)2 / p (p is the number of predictors)
Error variance: SSerror / dferror Σ(y-ybar)2 / N-2 (N-2 are the degrees of freedom of e)
- VAF = 1 - (SSerror / SStotal) --> SSy = s2y* dftotal
For simple linear regression also holds: VAF = r2
Significance testing:
- μy= β0 + β1x with variation σ
11.--> β0 is estimated with b0, β1is estimated with b1, σ is estimated with se.
- t = b1 / SEb1 SEb1 = se /sx √N-1 -
- Confidence interval for b1: b1± t * SEb1, where t* is two-tailed critical t value with df=N-2
- If p < 0.05, X is a significant predictor of Y.
- Testing significance of two independent regression weights: (b1.1means b1 in sample 1)
t = b1.1 - b1.2 / sb1.1-b.1.2 df = n1+ n2– 4 sb1.1-b1.2 = √s2e.1 / s2x.1 (N1 - 1) + s2e.2/ s2x.2 (N2 - 1)
Lecture 3
20/2/2019
- With multiple linear regressions, we have 1 response variable (y) and multiple predictor variables (x1, x2, et cetera). When we have more predictor variables, we will be able to estimate the response variable better and deal with less error variance. The multiple predictor variables do have to be related.
- Regression equation sample: y^ = b0 + b1x1 + b2x2 ... + bpxp
Regression equation population: μy = β0 + β1x1 + β2x2 ... + βpxp
- In multiple linear regression, the regression coefficient indicates the effect of x on y while controlling for the other predictor variables/keeping the other predictor variables constant.
- With two predictors, the relationship can be represented by a regression plane (a 3D scatterplot). The vertical distance from a point (y) to the plane ( is the error ei).
- Variances (mean squares):
-> Total variance: MSy = SSy / dfy = Σ(yhat-ybar)2 / N-1
Model variance: MSyhat = SSyhat/ dfyhatl = Σ(yhat-ybar)2 / p
Error variance: MSe = SSerror / dferror = Σ(y-ybar)2 / N-2
- VAF (Proportion Explained Variance): SSyhat / SSy VAF = R2
- R = the correlation between and y, the multiple correlation coefficient.
R2= the proportion explained variance / VAF
R2adj = the estimate of proportion explained variance in the population;
- Testing the regression model:
1) H0: R2= 0 Ha: R2> 0
H0: β1= β2= 0 Ha: at least one βj ≠ 0
H0: R = 0 HaR > 0 (cannot be negative)
2) ANOVA F-test for regression: F (dfyhat, dfe) = MSyhat / MSe with dfyhat = p and dfe= N – p – 1
Notes: in simple regression F is equal to t2, but not in multiple regression.
- F is a test statistic, like t or z. It looks at the ratio between unexplained and explained variance; the larger the test statistic, the smaller the p-value. F is always a positive value, since variances cannot be lower than 0.
3) Look up the F-value in the table to get a p-value.
4) Draw the statistical and substantive conclusion: If p < α, H0 is rejected and the results of the regression indicate that the two predictors collectively explain the VAF.
- Adding up the VAF of two predictors through simple regression analysis gives an other value than the VAF of these predictors through multiple regression. This is because one predictor explains a part of the variance of the response variable that the other predictor does too
- Semipartial correlation:
r0(1.2)= the correlation between y and part of x1that is independent of x2, so in other words the correlation between y and partly x1after correcting for the overlapping part with x2.
Semi-partial correlations in SPSS --> “Part correlations”
r0(1.2) = √ B / A+B+C+D
-Partial correlation:
r01.2= the correlation between y and part of x1that are both independent of x2:
r01.2 = √ B / A+B
- Testing the Multiple Regression Coefficient:
H0: βj= 0 Ha: βj≠ 0 / Ha: βj< 0
t = bj / SEbj with dfe= N – p – 1
--> Look up p-value in t-table and draw conclusions about the significance of predicting y for each of the predictor variables.
Confidence Interval for bj: bj ± t × SEbj
- Predict Y from X1and X2
Simple regression: Response variable (Y) and predictor (X; one of both)
Multiple regression: Response variable (Y) and predictors (X1 and X2)
-Spurious relations can be the result of a relation between X1and X2if we’ve only dealt with the relation between X1and Y. Controlling for X2should eliminate this spurious effect. We do this by using a multiple regression analysis.
Lecture 4
28/2/2019
- Assumptions for regression analysis:
--> Linearity: There is a linear relation between the predictor variables and the response variable.
--> Homoscedasticity: The variance of the residuals is equal for each predicted value. In a scatterplot showing homoscedasticity, the point are randomly distributed around a horizontal line. For heteroscedasticity, the point cloud varies in width; isn’t concentrated around a horizontal line.
--> Normality of the residuals: The residuals are normally distributed for every predicted value.
- When any of these assumptions are violated, the variable needs to be transformed. It this isn’t effective ~> restraint interpreting tests.
- With multicollinearity, two or more predictor variables are strongly intercorrelated (with an r higher than 0.70 or 0.80). Consequently, regression coefficients become unstable and standard errors increase. It is more difficult to find significant effects.
- Check: Tolerance: 1 – R2(as high as possible)
Variance Inflation Factor (VIF): 1 / tolerance (as low as possible)
If the tolerance is much larger than 0.10, and the VIF is much smaller than 10, there is no multicollinearity.
- If multicollinearity does exist, a variable needs to be removed from the regression model or predictors need to be combined into a sum score/scale.
- Test whether there are outliers on your data:
1) Distance: are the scores on Y much higher/lower than expected (look at the standardized residuals; higher than |3| are outliers).
2) Leverage: are there outliers on the predictors? (look at leverage values; 3(p+1) / N --> outlier on predicto
3) Influence: how much does an observation influence the results? (values smaller than 1 on Cook’s Distance are not influential).
- Is there no apparent reason for your outliers? Do not remove them! Apparent reason for removing outliers can be that it’s about an impossible score (due to data entry errors) or that it’s about an observation than is very different (e.g. a male in a female sample by accident).
-Selection methods:
Standard (Enter): All predictors are added simultaneously.
Stepwise: Predictors are added on the basis of their unique VAF
Hierarchical: Predictors are added in an order determined by the researcher.
-Confidence Interval (CI): μ^ ± t* × SEμ^
with SEμ^: se= √1/N + (x-xbar)2 / (N-1)s2x
and t* from t table with df = N – p – 1
-Prediction Interval (PI): y^ ± t* SEy^
with SEy^: se= √1 + 1/N + (x-xbar)2 / (N-1)s2x
and t* from t table with df = N – p – 1
- The predictor interval is always wider then the confidence interval. Intervals get wider as they get further away from the xbar.
-Mediation: When a predictor X indirectly affects the response Y.
Moderation: When the strength of the relation between X and Y depends on another variable.
Lecture 5
6/3/2019
- During this lecture, all the topics of the past lectures were reviewed.
New topics:
- During regression analysis, categorical variables can be included using dummy variables, which are dichotomous variables with 0 and 1. Advantages: look at differences between groups (means) and look for possible interaction.
- Testing interaction uses the same testing procedure as with testing two independent regression coefficients (see lecture 2).
Lecture 6
13/3/2019
- The problem of analysing multiple t-test to draw one conclusion is that the probability of Type I error increases (more about this effect will be explained in next week’s lecture), so we use Analysis Of Variance (ANOVA).
- ANOVA hypotheses: H0: μ1= μ2= ... μI
Hα: NOT μ1= μ2= ... μI
So what the ANOVA test does, is determining whether all the population means are equal or if there is a difference between at least two of them (= omnibus test).
- 1 categorical X variable --> One-way ANOVA
2 or more categorical X variables --> Factorial (or two-way) ANOVA
- The F-test compares differences between groups (explained) with differences within groups (unexplained).
- One-way ANOVA model:
Data (total) = Fit (between) + Residual (within)
yij = μi + εij
yij = μ + αi + εij
In which i = condition, j = participant, αi = effect parameter (= the effect of a certain condition compared to the grand mean); (μi – μ)
- Parameters in One-way ANOVA:
yij = μi + εij
yij = μ + αi + εij
- μ is estimated with ybar, μi is estimated with ybari , αi is estimated with α^ = ybari - ybar and σ is estimated with sp.
- Assumptions of the ANOVA model:
1. Homogeneity of variances
The variance of residuals is same in all populations: The rule of thumb is the largest sd / smallest sd < 2, or you can check the significance of Levene’s test.
2. Normality of the residuals
The residuals are normally distributed within each group (mean 0 and standard deviation σ): Look at histogram or P-P / Q-Q-plot of the residuals.
3. Independence
The residuals are independent: This should be guaranteed by the design of the study.
If the assumptions of homogeneity and/or normality are violated, you have to check the data set for error and outliers, or transform the Y variable or use a non-parametric test (Kruskal Wallis).
- Kruskal Wallis test hypotheses:
H0: MR1= MR2= ... MRI
Hα: NOT MR1= MR2= ... MRI
- ANOVA table:
Source Sum of Squares df Mean Square F
Groups SSG dfG SSG / dfG MSG / MSE
Error SSE dfE SSE / dfE
Total SST dfT SST/ dfT
The F-test looks at the ratio between explained (groups) and unexplained (error) variance:
F = MSG/ MSEwith dfGand dfE.
- SST= Σ (yij - )2 (difference between individual scores and grand mean)
> with df: N – 1
SSG= Σ ni(yij - )2= Σ ni α^i (differences between group means and grand mean)
> with df: I – 1 (I is the number of conditions/groups)
SSE= Σ (yij - i)2 (difference between individual scores and group means)
> with df: N – 1
- So: 
(Source: Lecture slides week 6, slide 17, Hemmo Smit, Leiden University)
- Note that SST= SSG+ SSE, dfT= dfG+ dfE; but MST≠ MSG+ MSE
- When p < α, the F test has showed that the groups are significantly different.
- Measures of effect size:
VAF in ANOVA is denoted by η2 instead of R2 η2= SSG/ SST
- η2 is based on sample statistics, but consequently overestimates the population value. Therefore we use ω^2: ω^2= SSG– (dfG* MSE) / SST+ MSE
This value is always lower than η2.
- Conclusion: estimated that in our population the 'between groups-factors explain ω^2 (percentage value) of the variance in Y.
- Rules of thumb for the effect size: small: .01 medium: .06 large: .14
Lecture 7
20/3/2019
- Why we cannot use results of multiple t-test to compare more than two group means:
Type I error is rejecting H0when it was in fact correct. When we perform multiple t-tests, we get an increased type I error.
-Familywise error: αfam = 1 – (1-α)c in which c = the number of comparisons.
- Solution: ANOVA F test; this compares all means simultaneously, so there is no increased type I error.
- ANOVA tests give us indications whether at least two group means differ significantly from each other. However, we don’t know which ones:
- To know which group means are significantly different from one another we can make:
- A priori comparisons; contrasts (planned comparisons)
Contrasts are specified before the data is collected.
- A posteriori comparisons; post-hoc comparisons
Additional test done after significant F-value is found to determine which means are significantly different.
- Examples for a priori hypotheses:
H0: (μ1 +μ2) / 2 = μ3 Hα: (μ1+μ2) / 2 > μ3 (one-sided)
H0: μ1= μ2 Hα: μ1≠ μ2 (two-sided)
- To determine a priori contrasts we formulate linear contrasts (ψ): combination of population means. The goal is to compare (groups of) means.
ψ = α1μ1+ α2μ2+ ... αkμk (αi are contrast coefficients)
- These contrast coefficients are weights. Groups with positive coefficients are compared with groups with negative coefficients. Contrast coefficients can be multiplied, as long as it’s with the same value, so that: Σαi = 0.
- Contrast can or cannot be orthogonal; independent. Criteria for being orthogonal:Σαi= 0, Σbi= 0, Σαibi= 0, and the number of comparisons: DFG = I – 1.
- t-test for contrasts:t = c / SEc = Σα1xbari / sp √Σα2i/ ni with df = DFE = N – 1
c = sample contrast
SEc= standard error of sample contrast
sp= pooled standard deviation (equal to √MSE)
- For testing a significant ANOVA F-test is not required.
- Contrasts in SPSS: Analyze --> Compare Means --> One-way ANOVA --> Contrasts
Specify αis one by one (Coefficients --> Add). With “Next” it is possible to specify multiple contrasts. αis should always add up to zero (the Coefficient Total).
- Conclusion: when p < α, y did not significantly differ between group 1 and group 2. Or: when p < α, y significantly differed for group 1 compared to the other groups.
- Other contrasts in SPSS: simple (first): each group is compared with the first group.
simple (last): each group is compared with the last group.
repeated: each group is compared with the next group.
polynomial: look at trend in data (linear, cubic, et cetera).
-Bonferroni Correction: corrects for when testing multiple contrast leads to an increased probability of Type I error.
α’ = α/c (c = number of comparisons)
Compare the p value with this corrected α. Using the Bonferroni Correction does decrease the power.
-Post-hoc tests are additional test (pairwise comparisons) that are done when the F-test is significant, but no specific hypotheses were formulated.
- There are multiple different tests:
--> Bonferroni corrections are done for a priori tests (a more conservative method; so we loose more power): α is adjusted by dividing it by the number of comparisons.
m (m-1) / 2 (m = the number of conditions)
--> Tukey corrections are done for post hoc tests. It essentially does the same thing as Bonferroni.
In SPSS: One Way ANOVA --> Contrasts --> Bonferroni / Tukey
- t** indicates a corrected t variable.
Lecture 8
27/3/2019
- Factorial designs include multiple independent variables.
- The outcome indicates the main effects; overall effect of each factor separately, and the interaction effects; the effect of one factor dependent upon the level of the other factor.
- Advantages of factorial designs:
1. Improved generalizability; by controlling for a hidden variable
2. More efficient research; better than doing two separate experiments with same number of participants per condition.
3. Increased power; the second factor in the model leads to a smaller error variance.
4. Interaction; investigates the interaction between two variables.
- One-way model: yij = μ+ αi + εij
where i = condition and j = participant.
- Factorial model: yijk = μ + αi + βj + αβij + εijk
where i = condition factor A, j = condition factor B and k = participant
μ is estimated with ybar
μijis estimated with ybarij
αiis estimated with α^i = ybari- ybar
βjis estimated with β^j= ybarj - ybar
αβijis estimated with α^βij = ybarij – (ybar+ α^i+ β^j)
σ is estimated with sp
- (Checking) assumptions in factorial ANOVA:
1) Homogeneity of variances; variances of residuals is the same in all populations:
largest sd / smallest sd < 2 or check Levene’s test.
2) Normality of residuals; residuals are normally distributed within each group
Check with the histogram or P-P/Q-Q plot of the residuals
3) Independence of residuals
Is guaranteed by the design.
- ANOVA table: 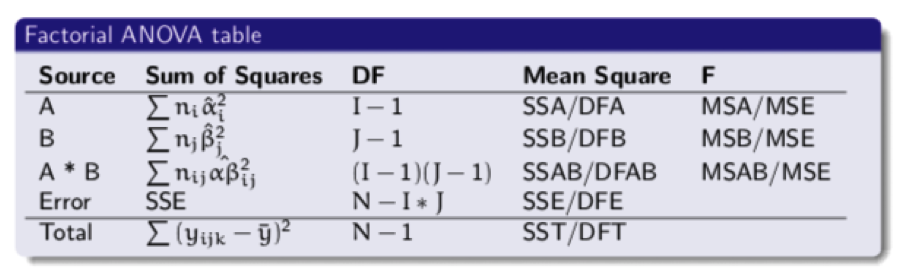
(Source: Lecture slides week 8, slide 11, Hemmo Smit, Leiden University)
- F-test looks at the ratio between explained effect and unexplained variance:
F = MSeffect/ MSE with dfeffectand dfE
- SS (Corrected Total) = SS (Corrected Model) + SS(Error)
SST = SSM + SSE
- Effect size for factorial ANOVA:
> Total VAF in sample: η2= SSM / SST
> VAF by effect in sample: η1= SSeffect/ SST
η2partial= SSeffect/ (SSeffect + SSE)
Rules of thumb: 0.01 = small 0.06 = medium 0.14 = large
> Estimated VAF by effect in population: ω^2= SSeffect – (dfeffect * MSE) / SST + MSE
Join with a free account for more service, or become a member for full access to exclusives and extra support of WorldSupporter >>

Contributions: posts
Spotlight: topics
JoHo can really use your help! Check out the various student jobs here that match your studies, improve your competencies, strengthen your CV and contribute to a more tolerant world










Exam Tips JulitaBonita contributed on 07-03-2019 11:12
A now 2nd year IBP student, shared her exam tips for this course last year. Check out the relevant content > IBP Leiden-Experimental and Correlational Research. You can also follow Ilona's profile for more summaries, blogs and lecture notes.
Workgroup notes Experimental and Correlational Research Psychology Supporter contributed on 28-03-2019 16:20
Another 1st year student is uploading her workgroup notes for the same course, useful complementary material > Check out Emy's profile for her content! :)
Add new contribution